Cho 2 đường thẳng MN và PQ cắt nhau tại A có MAQ = 80 độ. Tính MAP và PAN

Những câu hỏi liên quan
Hai đường thẳng MN và PQ cắt nhau tại A. Biết rằng M A Q ^ = 80 ° . Tính M A P ^ và P A N ^ .
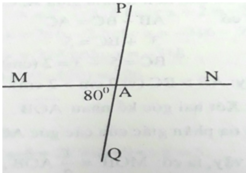
Ta có: M A Q ^ và M A P ^ kề bù nên:
M A Q ^ + M A P ^ = 180 °
80 ° + M A P ^ = 180 °
M A P ^ = 180 ° - 80 ° = 100 °
Và M A P ^ và P A N ^ kề bù nên:
M A P ^ + P A N ^ = 180 °
100 ° + P A N ^ = 180 °
P A N ^ = 180 ° - 100 ° = 80 °
Đúng 0
Bình luận (0)
Hai đường thẳng MN và PQ cắt nhau tại A. Biết rằng ∠MAQ= 80 0 . Tính ∠MAP và ∠PAN.
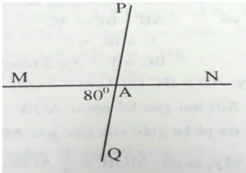
Ta có: ∠MAQ và ∠MAP kề bù nên:
∠MAQ + ∠MAP = 180 0
80 0 + ∠MAP = 180 0
∠MAP = 180 0 - 80 0 = 100 0
Và ∠MAP và ∠PAN kề bù nên:
∠MAP + ∠PAN = 180 0
100 0 + ∠PAN = 180 0
∠PAN = 180 0 - 100 0 = 80 0
Đúng 0
Bình luận (0)
Hai đường thẳng MN, PQ cắt nhau tại A tạo thành góc MAP = 33 độ Tính số đo góc MAQ và NAQ
Vì 2 đường thẳng MN,PQ cắt nhau tạo thành ^MAP=33 độ
⇒^MAP=^NAQ=33 độ
^MAQ+^MAP=180 độ (kề bù)
⇒^MAQ=180-^MAP
⇒^MAQ=180-33
⇒^MAQ=147 độ
Đúng 0
Bình luận (0)
Hai đường thẳng MN và PQ cắt nhau tại A tạo thành góc MAP có số đo góc bằng 33o
Tính số đo góc MAQ
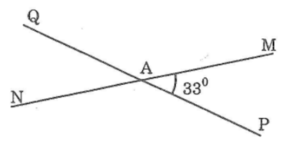
∠PAM và ∠MAQ là hai góc kề bù nên ∠PAM + ∠MAQ=180o
Suy ra: ∠MAQ = 180o-∠PAM =180o-33o=147o
Đúng 0
Bình luận (0)
Hai đường thẳng MN và PQ cắt nhau tại A.Góc MAQ=80 độ.Tính góc MAP và góc PAN
Hãy giúp mình nhé
Bn ơi, đây là trang văn mà
Lần sau đăng đúng chủ đề một chút
Đúng 0
Bình luận (0)
Hai đường thẳng MN và PQ cắt nhau tại A tạo thành góc MAP = 60• a/ tính MAQ và NAQ b/ gọi AH, Ak lần lượt là hai tia phân giác QAN và MAP. Chứng tỏ NAM và MAK là hai góc đối đỉnh c/ Trên một nửa mặt phẳng có bờ MN có chứa tia AQ về tia AO sao cho MAO = 90•. Chứng minh AO và AN ?
a: \(\widehat{MAQ}=180^0-60^0=120^0\)
\(\widehat{NAQ}=60^0\)
Đúng 0
Bình luận (0)
2 đường thẳng MN và PQ cắt nhau tại A tạo thành góc MAP có số đo bằng 33 độ.
a, Tính số đo góc NAQ.
b, Tính số đo góc MAQ.
c, Viết tên các cặp góc đối đỉnh.
d, Viết tên các cặp góc bù nhau.
3) Cho hai đường thẳng MN và PQ cắt nhau tại A tạo thành góc MAP có số đo bằng 450.
a) Tính số đo góc NAQ.
b) Tính số đo góc MAQ .
c Viết tên các cặp góc đối đỉnh.
d) Viết tên các cặp góc kề bù nhau.
a) Ta có:
∠MAP= ∠NAQ (hai góc đối đỉnh)
⇒ ∠NAQ = 45o
⇒ ∠NAQ = 45o
b) Ta có:
∠MAP + ∠MAQ = 180o ( hai góc kề bù )
⇒ 45o + ∠MAQ = 180o
⇒ ∠MAQ = 180o − 45o = 135o
c) Các cặp góc đối đỉnh là:
∠MAP, ∠NAQ
∠NAP, ∠MAQ
d) Các cặp góc bù nhau là:
∠MAP, ∠NAP
∠MAP, ∠MAQ
∠NAQ, ∠NAP
∠NAQ, ∠MAQ
Đúng 2
Bình luận (0)
hai đường thẳng MN và PQ cắt nhau tại A tạo thành góc MAP = 33 độ .
a, viết tên các cặp góc đối đỉnh
viết tên các cặp góc bù nhau
b, tính số đo góc NAQ và góc MAQ
a,có góc NAQ= goc MAP hai góc đối đỉnh
mà góc MAP =33 độ
suy ra góc NAQ=33 độ b, có gocsMAP+goc MAQ=180 hai goc ke bu goc
MAQ=180‐33=147 độ c, MAP va QAN QAM va NAP d, MAP va MAQ QAN va NAP
Đúng 0
Bình luận (0)





















