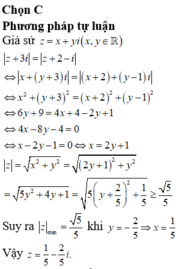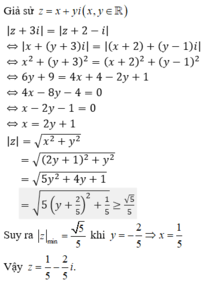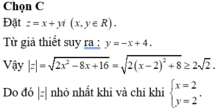an viêt số nhỏ nhất thỏa mãn điều kiện ;số đó là số chẵn có 4 cs, tổng các cs của số đó = 10.tìm số đó

Những câu hỏi liên quan
Cho số phức z thỏa mãn điều kiện
z
-
3
+
2
i
z
-
i
Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
Đọc tiếp
Cho số phức z thỏa mãn điều kiện z - 3 + 2 i = z - i Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
![]()
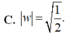
![]()
Tìm số phức z có môđun nhỏ nhất thỏa mãn điều kiện
z
4
+
5
z
2
+
4
0
A.
3
5
-
6
5
i
B.
6
5
-
3
5
i
C.
9
5
D....
Đọc tiếp
Tìm số phức z có môđun nhỏ nhất thỏa mãn điều kiện z 4 + 5 z 2 + 4 = 0
A. 3 5 - 6 5 i
B. 6 5 - 3 5 i
C. 9 5
D. 3 5 5
Gọi z = a + bi
Ta có
- 2 - 3 i + z = z - i ⇔ a - 2 - b + 3 i = a + b - 1 i ⇔ a - 2 2 + b + 3 2 = a 2 + b - 1 2 ⇔ a = 2 b + 3
Ta cần tìm z sao cho a 2 + b 2 đạt giá trị nhỏ nhất.
Ta có
a 2 + b 2 = 2 b + 3 2 + b 2 = 5 b + 6 5 2 + 9 5 ≥ 9 5
Do đó m i n a 2 + b 2 = 9 5 ⇔ b = - 6 5 , a = 3 5
Vậy 3 5 - 6 5 i
Đáp án A
Đúng 0
Bình luận (0)
Số nguyên a nhỏ nhất thỏa mãn điều kiện \(6< 2\sqrt{a+1}-2\) là số nào?
\(6< 2\sqrt{a+1}-2\Leftrightarrow8< 2\sqrt{a+1}\Leftrightarrow4< \sqrt{a+1}\Leftrightarrow16< a+1\Leftrightarrow15< a\)
Mà a là số nguyên nhỏ nhất nên \(a=16\)
Đúng 1
Bình luận (0)
Cho cấp số nhân
b
n
thỏa mãn
b
2
b
1
≥
1
và hàm số thỏa mãn điều kiện
f
x
x
3
-
3
x
Giá trị nhỏ nhất của n để
b
n
5
100
bằng A. 234 B. 229...
Đọc tiếp
Cho cấp số nhân b n thỏa mãn b 2 > b 1 ≥ 1 và hàm số thỏa mãn điều kiện f x = x 3 - 3 x Giá trị nhỏ nhất của n để b n > 5 100 bằng
A. 234
B. 229
C. 333
D. 292
Trong các số phức thỏa mãn điều kiện
z
+
3
i
z
+
2
-
i
Tìm số phức có môđun nhỏ nhất ? A. z 1 -2i B. z
-
1
5
+
2
5
i
C. z
1
5...
Đọc tiếp
Trong các số phức thỏa mãn điều kiện z + 3 i = z + 2 - i Tìm số phức có môđun nhỏ nhất ?
A. z = 1 -2i
B. z = - 1 5 + 2 5 i
C. z = 1 5 - 2 5 i
D. z = -1+2i
Trong các số phức thỏa mãn điều kiện
|
z
+
3
i
|
|
z
+
2
-
i
|
.
Tìm số phức có môđun nhỏ nhất? A.
z
1
-
2
i
B.
z
-
1
5
+
2...
Đọc tiếp
Trong các số phức thỏa mãn điều kiện | z + 3 i | = | z + 2 - i | . Tìm số phức có môđun nhỏ nhất?
A. z = 1 - 2 i
B. z = - 1 5 + 2 5 i
C. z = 1 5 - 2 5 i
D. z = -1 + 2i
Trong các số phức thỏa mãn điều kiện: z - 2 - 4 i = z - 2 i . Tìm số phức z có môđun nhỏ nhất
A. z = 2 +i
B. z = 3 +i
C. z = 2 +2i
D. z = 1 +3i
Trong các số phức thỏa mãn điều kiện z − 2 − 4 i = z − 2 i . Số phức z có môđun nhỏ nhất là
A. z = 2 - 2i
B. z = -1 + 5i
C. z = 2 + 2i
D. z = 1 + 2i
Trong các số phức z thỏa mãn điều kiện |z – 1 – 2i| 2, tìm số phức z có môđun nhỏ nhất.
Đọc tiếp
Trong các số phức z thỏa mãn điều kiện |z – 1 – 2i| = 2, tìm số phức z có môđun nhỏ nhất.
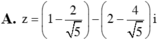
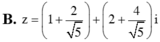
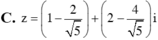
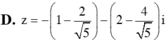
Chọn C.
Gọi z = x + yi và M (x; y) là điểm biểu diễn số phức.
Ta có : |z – 1 – 2i| = 2 hay ( x - 1) 2 + (y - 2)2 = 4
Đường tròn (C): ( x - 1)2 + (y - 2)2 = 4 có tâm I(1; 2). Đường thẳng OI có phương trình y = 2x
Số phức z thỏa mãn điều kiện và có môdun nhỏ nhất khi và chỉ khi điểm biểu diễn số phức đó thuộc đường tròn (C) và gần gốc tọa độ O nhất, điểm đó chỉ là một trong hai giao điểm của đường thẳng OI với (C), khi đó tọa độ của nó thỏa mãn hệ
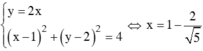 hoặc
hoặc 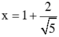
Chọn  nên số phức
nên số phức 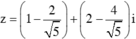
Đúng 0
Bình luận (0)