\(f\left(x\right)=\dfrac{4}{x}+\dfrac{x-1+1}{1-x}=\dfrac{4}{x}+\dfrac{1}{1-x}-1\)

\(f\left(x\right)\ge\dfrac{\left(2+1\right)^2}{x+1-x}-1=8\)

\(f\left(x\right)_{min}=8\) khi \(x=\dfrac{2}{3}\)

f(x) = x³ +3/x = x³ + 1/x +1/x +1/x 

cô si 4 số làm mất x là xong

Đề bị sai?

Đạo hàm f'(x) =  m 2 - m + 1 ( x + 1 ) 2 > 0,  ∀ x   ∈   [ 0 ; 1 ]  

Suy ra hàm số f(x)  đồng biến trên [0; 1] nên min f(x) = f(0) = -m²+m

Theo bài ta có:

-m²+ m= -2 nên m= -1 hoặc m= 2.

Chọn D.

Ta có f(x) đạt giá trị lớn nhất khi \(\frac{1}{f\left(x\right)}\) đạt giá trị nhỏ nhất.

Xét \(\frac{1}{f\left(x\right)}=\frac{x^2+2014x+1}{x}=x+\frac{1}{x}+2014\ge2\sqrt{x.\frac{1}{x}}+2014=2016\)

Dấu "=" xảy ra khi \(\hept{\begin{cases}x>0\\x=\frac{1}{x}\end{cases}}\Leftrightarrow x=1\)

 \(Min\)\(\frac{1}{f\left(x\right)}=2016\Leftrightarrow x=1\)

Vậy \(Max\)\(f\left(x\right)=\frac{1}{2016}\Leftrightarrow x=1\)

blabla..

Chọn D

Ta có  3x.f(x) -  x 2 f ' ( x )   =   2 f 2 ( x )  

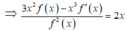
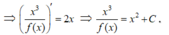
Thay x = 1 vào ta được 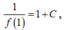 vì f(1) =  1 3 nên suy ra C = 2

Nên  Ta có: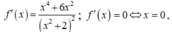 

Khi đó, f(x) đồng biến trên [1;2]

Suy ra 

Suy ra