Đạo hàm f'(x) = m 2 - m + 1 ( x + 1 ) 2 > 0, ∀ x ∈ [ 0 ; 1 ]
Suy ra hàm số f(x) đồng biến trên [0; 1] nên min f(x) = f(0) = -m2+m
Theo bài ta có:
-m2+ m= -2 nên m= -1 hoặc m= 2.
Chọn D.
Đạo hàm f'(x) = m 2 - m + 1 ( x + 1 ) 2 > 0, ∀ x ∈ [ 0 ; 1 ]
Suy ra hàm số f(x) đồng biến trên [0; 1] nên min f(x) = f(0) = -m2+m
Theo bài ta có:
-m2+ m= -2 nên m= -1 hoặc m= 2.
Chọn D.
Cho hàm số f(x) = 2 x + m x + 1 với m là tham số thực. Tìm tất cả các giá trị của m > 1 để hàm số có giá trị lớn nhất trên đoạn [ 0; 4] nhỏ hơn 3.
A. 1<m< 3
B. m ∈ ( 1 ; 3 5 - 4 )
C. m ∈ ( 1 ; 5 )
D. 1<m≤ 4
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Tìm tất cả các giá trị của tham số m để hàm số y = x + m x 2 + x + 1 có giá trị lớn nhất trên ℝ nhỏ hơn hoặc bằng 1.
A. m ≤ 1
B. m ≥ 1
C. m ≥ -1
D. m ≤ -1
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Cho hàm số \(f\left(x\right)=\frac{1}{5}m^2x^5-\frac{1}{3}mx^3+10x^2-\left(m^2-m-20\right)x\)Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên R. Tổng giá trị của tất cả các phần tử thuộc S bằng :
A. 3/2
B. -2
C. 5/2
D. 1/2
Cho hàm số y= x3- 3x+ 1 . Tìm tìm tập hợp tất cả giá trị m> 0 , để giá trị nhỏ nhất của hàm số trên D= [m+ 1; m+ 2] luôn bé hơn 3 là:
A. (0; 1)
B. ( 1 2 ; 1)
C. (2; 3)
D. (0; 2)
Cho hàm số f(x) có đạo hàm liên tục trên ℝ và thỏa mãn f(x) > 0, ∀ x ∈ ℝ . Biết f(0) = 1 và f ' ( x ) = ( 6 x - 3 x 2 ) f ( x ) . Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = m có nghiệm duy nhất.
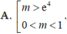
![]()
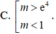
![]()
Gọi A, B là hai điểm cực trị của đồ thị hàm số f(x) = x3 - 3x2 + m với m là tham số thực khác 0. Tìm tất cả các giá trị thực của tham số m để trọng tâm tam giác OAB thuộc đường thẳng 3x + 3y - 8 = 0.
A. m = 5
B. m = 2
C. m = 6
D. m = 4
Gọi A, B lần lượt là các giá trị nhỏ nhất, giá trị lớn nhất của hàm số y= x + m 2 + 2 m x - 2 trên đoạn [3;4]. Tìm tất cả các giá trị thực của tham số m để A+B= 19 2
A. m=1; m=-3
B. m=-1; m=3
C. m=3; m= -3
D. m=-4