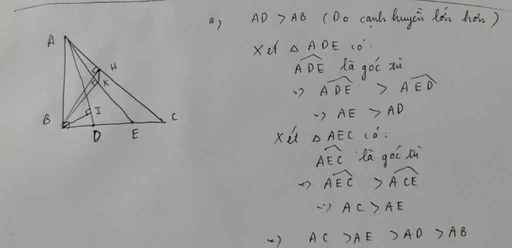cho ΔABC vuông ở A.Trên cạnh BC lấy D,E ∈ cạnh BC theo thứ tự
so sánh AD,AE,AC,AB

Những câu hỏi liên quan
cho ΔABC vuông ở A.Trên cạnh BC lấy D,E ∈ cạnh BC theo thứ tự
so sánh AD,AE,AC,AB
cho ΔABC vuông tại C (AC<AB) trên cạnh AB lấy điểm D sao cho AD=AC kẻ qua đường thẳng vuông góc với AB cách BC tại E. AE cách CD tại I
a) CMR: ΔADE = ΔACE
b) CM: AE là phân giác của góc CAB
c) so sánh EC và BE giúp tớ với!!!
a: Xét ΔADE vuông tại D và ΔACE vuông tại C có
AE chung
AD=AC
Do đó:ΔADE=ΔACE
b: Ta có: ΔADE=ΔACE
nên \(\widehat{CAE}=\widehat{DAE}\)
hay AE là tia phân giác của góc DAC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A.trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E. Hãy so sánh DE và BC
1,Cho tam giác ABC có AB < AC,AD là phân giác của góc A ( D thuộc BC ).Trên cạnh AC lấy điểm E sao cho AE = AB
a,CM:CD > BD
b,So sánh góc ADB và góc ADC
2,Cho tam giác ABC cân tại A.Trên cạnh AB lấy điểm D.Trên tia đối của tia CA lấy điểm E sao cho BD = CE.Nối D với E.Kẻ DH vuông góc với BC ( H thuộc BC ),EK vuông góc với BC ( K thuộc BC ).CM:
a,BH = CK
b,BC < DE
1:
a: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB<AC
nên BD<CD
b: AB<AC
=>góc B>góc C
góc ADB=góc C+góc CAD
góc ADC=góc B+góc BAD
mà góc C<góc B và góc CAD=góc BAD
nên góc ADB<góc ADC
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A, AH ⊥ BC tại H. Trên cạnh BC lấy D sao cho BD = BA. Đường vuông góc với BC tại D cắt AC ở E
a) So sánh AE và DE
b) Chứng minh tia AD là tia phân giác của góc HAC
c) Vẽ DK vuông góc với AC tại K. Chứng minh rằng AK = AH
a, vì BD=BA nên t.giác DBA caab tại B
=>\(\widehat{BDA}\)=\(\widehat{BAD}\)mà \(\widehat{EDB}\)=\(\widehat{A}\)=90 độ nên suy ra góc \(\widehat{EAD}\)=\(\widehat{EDA}\)
=>t.giác EAD cân tại E
=>AE=DE đpcm
b,vì ED và AH cùng vuông góc vs BC nên ED//AH
=> \(\widehat{EDA}\)=\(\widehat{DAH}\)(so le) mà \(\widehat{EDA}\)=\(\widehat{EAD}\)(t.giác AED cân tại E)
=>\(\widehat{DAH}\)=\(\widehat{EAD}\)
=> AD là p/g của góc HAC
c, xét 2 t.giác vuông AKD và AHD có:
AD chung
\(\widehat{KAD}\)=\(\widehat{HAD}\)(AD là p/g của \(\widehat{HAC}\))
=>t.giác AKD=t.giác AHD(CH-GN)
=>AK=AH
#HỌC TỐT#
Đúng 0
Bình luận (0)
Cho ΔABC có AB <AC . Tia phân giác góc A cắt BC ở D. Trên cạnh AC lấy điểm E sao cho AB =AE
So sánh BD và DC
Cho ΔABC có AB
So sánh BD và DC
Đề thiếu mk ko làm được
Cho tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên.Gọi M là trung điểm của BC.
a:Cm AM vuông góc với BC
b:Trên cạnh AB và AC lấy điểm D và E theo thứ tự sao cho AD=AE. Cm DE//BC
Câu a là tính chất của tam giác cân mà bạn nếu cần thì bạn cm như sau:
Xét tam giác ABM và ACM có :
AM chung
AB=AC ( tam giác ABC cân ở A )
Bm=MC (GT)
=> hai tam giác = nhau
=> góc AMB= góc AMC mà tổng hai góc đó = 180 độ
=> AMB=90 độ Hay AM vuông góc với BC
B,Vì tam giác ADE và ABC đều cân ở A
Mà Có DAE=BAC => ADE=ABC (hai góc đồng vị = nhau ) => DE//BC
Đúng 0
Bình luận (0)
a) Xét \(\Delta ABM\) và \(\Delta ACM\) có:
\(AB=AC\)(gt)
\(\widehat{ABM}=\widehat{ACM}\) (gt)
\(BM=CM\)(gt)
suy ra: \(\Delta ABM=\Delta ACM\)(c.g.c)
\(\Rightarrow\)\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\) (kề bù)
\(\Rightarrow\)\(\widehat{AMB}=\widehat{AMC}=90^0\)
\(\Rightarrow\)\(AM\)\(\perp\)\(BC\)
b) \(\Delta ADM\)cân tại A (do AD = AE)
\(\Rightarrow\)\(\widehat{ADE}=\frac{180^0-\widehat{A}}{2}\) (1)
\(\Delta ABC\)cân tại A
\(\Rightarrow\)\(\widehat{ABC}=\frac{180^0-\widehat{A}}{2}\) (2)
Từ (1) và (2) suy ra: \(\widehat{ADE}=\widehat{ABC}\)
\(\Rightarrow\)\(DE\)\(//\)\(BC\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại B. Trên cạnh BC lấy các điểm D và E (D nằm giữa B và E).
a)So sánh độ dài các đoạn thẳng AB, AD, AE, AC.
b)Vẽ BI, BK, BH lần lượt vuông góc với AD, AE, AC. So sánh các góc ABH, ABK, ABI.
Cho tam giác ABC vuông tại B. Trên cạnh BC lấy các điểm D và E (D nằm giữa B và E).
a) So sánh độ dài các đoạn thẳng AB, AD, AE, AC
b) Vẽ BI, BK, BH lần lượt vuông góc với AD, AE, AC. So sánh các góc ABH, ABK, ABI.