Trong mặt phẳng Oxy, cho hình vuống ABCD tâm I.Gọi M,N lần lượt là trung điểm của AB, IC. Giả sử M(1;2) N(-2;5). Viết phương trình đường thẳng CD
Trong mặt phẳng toạ độ Oxy cho hình vuông ABCD tâm I. Gọi M, N lần lượt là trung điểm
của AB, IC. Giả sử M(1;2), N(-2; 5). Viết phương trình đường thẳng CD.
Trong mặt phẳng Oxy , cho hình vuông ABCD tâm I . Gọi M,N lần lượt là trung điểm của AB , IC . Giả sử M(1;2) , N(-2;5) . Viết phương trình đường thẳng CD ?
Trong mặt phẳng toạ độ Oxy cho hình chữ nhật ABCD tâm I có AB = 2AD . Gọi M là trung điểm AB và N là điểm thuộc đoạn AC sao NC = 4IN . Giả sử M(2;5), N(1;7). Viết phương trình đường thẳng CD.
Trong mặt phẳng tọa độ oxy cho hình bình hành ABCD có A(0,8). Trung điểm các cạnh DC, BC lần lượt là M(4;-1) và N(2;5). Tìm G là trọng tâm tam giác ABC?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M, N lần lượt là trung điểm của AB, AD. Giả sử C N ∩ D M Biết SH = 2a và vuông góc với mặt phẳng (ABCD). Khi đó thể tích S.CDMN
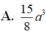
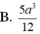
![]()
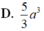
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có I là giao điểm của hai đường chéo AC và BD. Gọi M (3; 2) và N (1; —2) lần lượt là trung điểm của đoạn AB và ID. Tìm phương trình tổng quát của đường thẳng AB.
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có I là giao điểm của hai đường chéo AC và BD. Gọi M (3; 2) và N (1; —2) lần lượt là trung điểm của đoạn AB và ID. Tìm phương trình tổng quát của đường thẳng AB.
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có I là giao điểm của hai đường chéo AC và BD. Gọi M(3;2) và N(1;-2) lần lượt là trung điểm của các đoạn AB và ID. Tìm phương trình tổng quát của đoạn thẳng AB.
tham khảo
Gọi M' là điểm đối xứng của M qua AC. Ta có M' thuộc đường thẳng BC.
Phương trình đường thẳng MM' là 1(x - 6) - 1(y - 2) = 0 <=> x - y - 4 = 0. Gọi H = AC ∩ MM'
Tọa độ của H thỏa mãn hệ 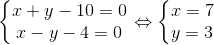 => H(7; 3)
=> H(7; 3)
H là trung điểm của MM'. Suy ra M'(8; 4)
Gọi 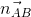 = (a; b) . Vì hai đường thẳng AB và AC tạo với nhau một góc 450 nên ta có:
= (a; b) . Vì hai đường thẳng AB và AC tạo với nhau một góc 450 nên ta có:
cos 450 = 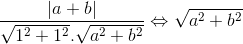 = |a + b| ⇔ ab = 0
= |a + b| ⇔ ab = 0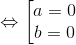
TH1: a = 0, phương trình đường thẳng AB, BC lần lượt là y = 8, x = 8. Suy ra: B(8; 8)
TH2: b = 0, phương trình đường thẳng AB, BC lần lượt là y = 5, x = 4. Suy ra: B(5; 4)
Trong mặt phẳng Oxy, cho tam giác ABC có B(1,3), C(5,-1). Gọi M, N lần lượt là trung điểm của AB và AC. Tìm tọa độ trọng tâm G của tam giác ABC.