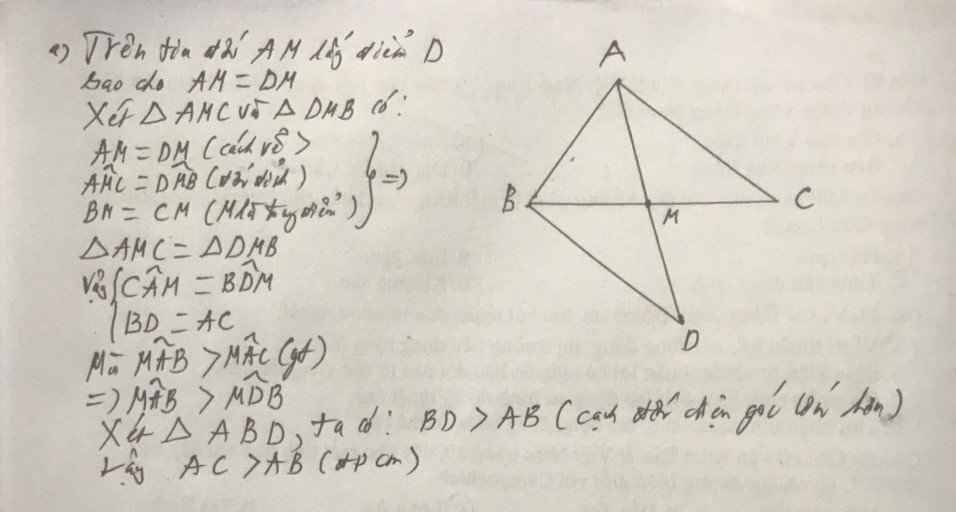Gọi M là TĐ của BC của tam giác ABC. CM: AC>AB⇔∠MAB>∠MAC.

Những câu hỏi liên quan
Gọi M là TĐ của BC trong tam giác ABC. CM: AC>AB hay góc MAB> MAC
Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. Chứng minh MAB ^ > MAC ^
Tam giác ABC có M là trung điểm của BC
a) Biết góc MAB>góc MAC. Chứng Minh :AC>AB
b) Biết AC > AB chứng minh góc MAB > góc MAC
Gọi M là trung điểm của BC, CỦA TAM GIÁC ABC
CMR AC > AB suy ra : góc MAB > MAC
Cho tam giác ABC có AB : AC : BC = 4: 5: 6 và chu vi tam giac bằng 30 cm
a)So sánh các góc của tam giác.
b)Gọi M là trung điểm của BC, so sánh các góc MAB và MAC.
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AB}{4}=\dfrac{AC}{5}=\dfrac{BC}{6}=\dfrac{AB+AC+BC}{4+5+6}=\dfrac{30}{15}=2\)
Do đó: AB=8cm; AC=10cm; BC=12cm
=>\(\widehat{C}< \widehat{B}< \widehat{A}\)
b: \(\cos MAB=\dfrac{AB^2+AM^2-BM^2}{2\cdot AB\cdot AM}=\dfrac{AB^2+AM^2-CM^2}{2\cdot AB\cdot AM}\)
\(\cos MAC=\dfrac{AM^2+AC^2-MC^2}{2\cdot AM\cdot AC}\)
mà \(\dfrac{AB^2+AM^2-MC^2}{2\cdot AM\cdot AC}< \dfrac{AM^2+AC^2-MC^2}{2\cdot AM\cdot AC}\)
nên \(\widehat{MAB}>\widehat{MAC}\)
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A gọi M là TĐ BC trên tia đối của tia MA lấy điểm E sao cho MA= ME
a, Vẽ hình , nêu gt, kl
b,CM tam giác MAB = tam giác MEC
c, Vì sao AB// EC
d, CM tam giác BEC vuông tại
b: Xét ΔMAB và ΔMEC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)
MB=MC
Do đó: ΔMAB=ΔMEC
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB<AC. Gọi M là trung điểm của BC, CHỨNG MINH GÓC MAB>GÓC MAC. Từ đó suy ra p/giác của cóc BAC cắt cạnh BC tại 1 điểm nằm giữa B và M
Vẽ tam giác ABC có BC = 5 cm, AB = 4 cm, AC = 3 cm.
a) Nêu cách vẽ tam giác ABC
b) Cho góc CAB = 90 độ trên BC lấy M sao cho MAB = 5/4 MAC. Tính MAB
c) Trong góc MAB vẽ tia Ax cắt BC tại N sao cho góc NAB = 10 độ CMR AM là phân giác của góc NAC.
352465266865625555555555555665-1=
Cho tam giác ABC M là trung điểm của BC
a,biết góc ABM lớn hơn góc MAC CM AC>AB
b,biết AB>AC CM GÓc MAB lớn hơn góc MÂC
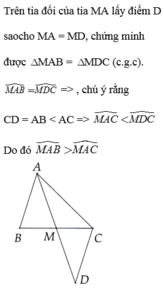
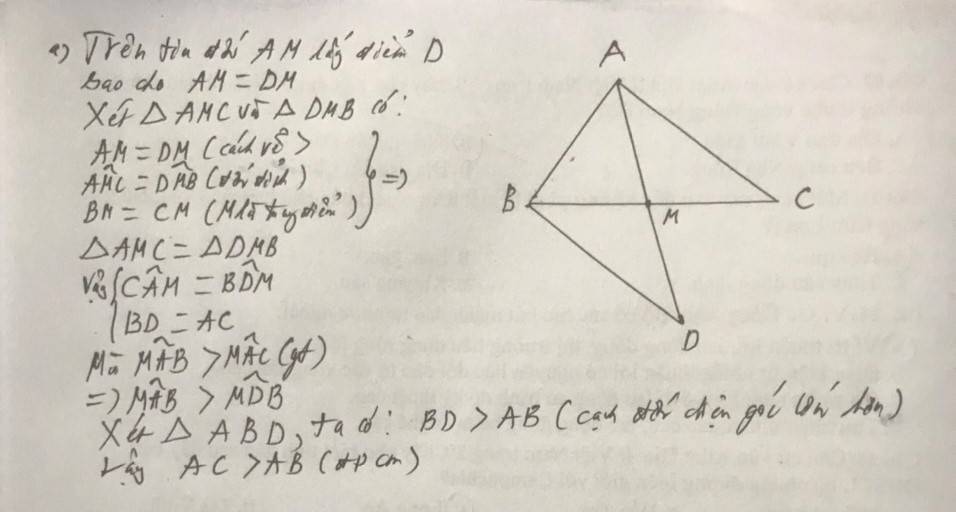
Trên tia đối tia MA lấy điểm D sao cho MD = MA Xét ΔAMB và ΔDMC, ta có: MA = MD (theo cách vẽ) ∠(AMB) = ∠(DMC) (đối đỉnh) MB = MC (gt) Suy ra: ΔAMB = ΔDMC (c.g.c) Suy ra: AB = CD (2 cạnh tương ứng) và ∠D = ∠A1(2 góc tương ứng) (1) Mà AB < AC (gt) nên: CD < AC Trong ΔADC, ta có: CD < AC Suy ra: ∠D > ∠A2(đối diện cạnh lớn hơn là góc lớn hơn) (2) Từ (1) và (2) suy ra: ∠A1 > ∠A2hay ∠(BAM) > ∠(MAC)
Đúng 0
Bình luận (0)