từ điểm M thuộc đường thẳng (d) ở ngoài (O) sao cho khoảng cách từ điểm O đến (d) bằng h ko đổi kẻ hai tiếp tuyến MA,MC đến (O). Gọi K là giao điểm của OM, AB. Chứng minh AB đi qua điểm cố định

Những câu hỏi liên quan
Cho đường tròn (O; R) và đường thẳng d không có điểm chung sao cho khoảng cách từ O đến d không quá 2R. Qua diêm M trên d, vẽ các tiếp tuyến MA, MB tới (O) với A, B là các tiếp điểm. Gọi H là hình chiếu vuông góc của O trên d. Vẽ Dây AB cắt OH ở K và cắt OM tại I. Tia OM cắt (O) tại E.a, Chứng minh OM
⊥
AB và OI.OM
R
2
b, Chứng minh OK.OH OI.OMc, Tìm vị trí của M trên d để OAEB là hình thoid, Khi M di chuyên trên d, c...
Đọc tiếp
Cho đường tròn (O; R) và đường thẳng d không có điểm chung sao cho khoảng cách từ O đến d không quá 2R. Qua diêm M trên d, vẽ các tiếp tuyến MA, MB tới (O) với A, B là các tiếp điểm. Gọi H là hình chiếu vuông góc của O trên d. Vẽ Dây AB cắt OH ở K và cắt OM tại I. Tia OM cắt (O) tại E.
a, Chứng minh OM ⊥ AB và OI.OM = R 2
b, Chứng minh OK.OH = OI.OM
c, Tìm vị trí của M trên d để OAEB là hình thoi
d, Khi M di chuyên trên d, chứng minh đường thẳng AB luôn đi qua một điểm cố định
a, Theo tính chất của hai tiếp tuyến cắt nhau chứng minh được OM là đường trung trực của AB, tức OM vuông góc AB. Áp đụng hệ thức lượng trong tam giác vuông OAM chứng minh được : OI. OM = O A 2 = R 2
b, Chứng minh được: ∆OKI:∆OMH(g.g) => OK.OH = OI.OM
c, Để OAEB là hình thoi thì OA = EB. Khi đó, tam giác OAK đều, tức là
A
O
M
^
=
60
0
. Sử dụng tỉ số lượng giác của góc
A
O
M
^
, tính được OM=2OA=2R, tức là M cách O một khoảng 2R
d, Kết hợp ý a) và b) => OK.OH =
R
2
=> OK =
R
2
O
H
Mà độ dài OH không đổi nên độ dài OK không đổi
Do đó, điểm K là điểm cố định mà AB luôn đi qua khi M thay đổi
Đúng 0
Bình luận (0)
Xét đường thẳng (d) cổ định ở ngoài (0;R) (khoảng cách từ 0 đến (d) không nhỏ hơn R2). Từ một điểm M nằm trên đường thắng (d) ta dựng các tiếp tuyến MA, MB đến (O:R) ( A,B là các tiếp điểm) và dựng cát tuyên MCD (tia MC nằm giữa hai tia MO, MA và MC MD). Gọi E là trung điểm của CD, H là giao điểm của AB và MO. a, Chứng minh: 5 điểm M,A,E,O,B cùng nằm trên một đường tròn. b, Chứng minh: MC.MD MA² MO² –R² . c. Chứng minh: Các tiếp tuyến tại C,D của đường tròn (O;R) cắt nhau tại một điểm nằm trên...
Đọc tiếp
Xét đường thẳng (d) cổ định ở ngoài (0;R) (khoảng cách từ 0 đến (d) không nhỏ hơn R2). Từ một điểm M nằm trên đường thắng (d) ta dựng các tiếp tuyến MA, MB đến (O:R) ( A,B là các tiếp điểm) và dựng cát tuyên MCD (tia MC nằm giữa hai tia MO, MA và MC < MD). Gọi E là trung điểm của CD, H là giao điểm của AB và MO. a, Chứng minh: 5 điểm M,A,E,O,B cùng nằm trên một đường tròn. b, Chứng minh: MC.MD= MA² = MO² –R² . c. Chứng minh: Các tiếp tuyến tại C,D của đường tròn (O;R) cắt nhau tại một điểm nằm trên đường thắng AB. d. Chứng minh: Đường thắng AB luôn đi qua một điểm cố định. e, Chứng minh: Một đường thắng đi qua O vuông góc với MO cắt các tia MA, MB lần lượt tại PQ. Tìm GTNN của SMPO. Tìm vị trí điểm M để AB nhỏ nhất.
1. cho đường tròn (O) và điểm M nằm ngoài (O). Từ điểm M kẻ hai tiếp tuyến MA,MC (A,C là các tiếp điểm ) tới đường tròn(O) .Từ điểm M kẻ cát tuyến MBD (B nằm giữa M và D, MBD ko đi qua O). gọi H là giao điểm của OM và AC . từ C kẻ đường thẳng song song với BD cắt đường tròn(O) tại E (E khác C) , gọi K là giao điểm của AE và BD . chứng minha, Tứ giác OAMC nội tiếpb, K là trung điểm của BDc, AC là phân giác của góc BHD
Đọc tiếp
1. cho đường tròn (O) và điểm M nằm ngoài (O). Từ điểm M kẻ hai tiếp tuyến MA,MC (A,C là các tiếp điểm ) tới đường tròn(O) .Từ điểm M kẻ cát tuyến MBD (B nằm giữa M và D, MBD ko đi qua O). gọi H là giao điểm của OM và AC . từ C kẻ đường thẳng song song với BD cắt đường tròn(O) tại E (E khác C) , gọi K là giao điểm của AE và BD . chứng minh
a, Tứ giác OAMC nội tiếp
b, K là trung điểm của BD
c, AC là phân giác của góc BHD
a) Xét tứ giác OAMC có
\(\widehat{OAM}\) và \(\widehat{OCM}\) là hai góc đối
\(\widehat{OAM}+\widehat{OCM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: OAMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
1. cho đường tròn (O) và điểm M nằm ngoài (O). Từ điểm M kẻ hai tiếp tuyến MA,MC (A,C là các tiếp điểm ) tới đường tròn(O) .Từ điểm M kẻ cát tuyến MBD (B nằm giữa M và D, MBD ko đi qua O). gọi H là giao điểm của OM và AC . từ C kẻ đường thẳng song song với BD cắt đường tròn(O) tại E (E khác C) , gọi K là giao điểm của AE và BD . chứng minha, Tứ giác OAMC nội tiếpb, K là trung điểm của BDc, AC là phân giác của góc BHD
Đọc tiếp
1. cho đường tròn (O) và điểm M nằm ngoài (O). Từ điểm M kẻ hai tiếp tuyến MA,MC (A,C là các tiếp điểm ) tới đường tròn(O) .Từ điểm M kẻ cát tuyến MBD (B nằm giữa M và D, MBD ko đi qua O). gọi H là giao điểm của OM và AC . từ C kẻ đường thẳng song song với BD cắt đường tròn(O) tại E (E khác C) , gọi K là giao điểm của AE và BD . chứng minh
a, Tứ giác OAMC nội tiếp
b, K là trung điểm của BD
c, AC là phân giác của góc BHD
a: góc OAM+góc OCM=180 độ
=>OAMC nội tiếp
b: CE//BD
=>góc AKM=góc AEC=góc ACM
=>AKCM nội tiếp
=>A,K,C,M cùng nằm trên 1 đường tròn
=>góc OKM=90 độ
=>K là trung điểm của BD
Đúng 0
Bình luận (0)
Từ một điểm M nằm ngoài đường tròn (O;R) kẻ hai tiếp tuyến MB MC đến đường tròn(o) sao cho MD<MA, C và D nằm ở hai nửa mặt phẳng khác nhau bờ OM. Gọi H là giao điểm của OM và BC .
chứng minh MH.MO=MD.MA
Xét (O) có
\(\widehat{MBD}\) là góc tạo bởi tiếp tuyến BM và dây cung BD
\(\widehat{BAD}\) là góc nội tiếp chắn cung BD
Do đó: \(\widehat{MBD}=\widehat{BAD}\)
Xét ΔMBD và ΔMAB có
\(\widehat{MBD}=\widehat{MAB}\)
\(\widehat{BMD}\) chung
Do đó: ΔMBD đồng dạng với ΔMAB
=>\(\dfrac{MB}{MA}=\dfrac{MD}{MB}\)
=>\(MB^2=MA\cdot MD\left(1\right)\)
Xét (O) có
MB,MC là các tiếp tuyến
Do đó: MB=MC
=>M nằm trên đường trung trực của BC(2)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(3)
từ (2),(3) suy ra MO là đường trung trực của BC
=>MO\(\perp\)BC tại H
Xét ΔMBO vuông tại B có BH là đường cao
nên \(MH\cdot MO=MB^2\left(4\right)\)
Từ (1),(4) suy ra \(MH\cdot MO=MD\cdot MA\)
Đúng 0
Bình luận (0)
cho đường tròn (O;R) và đường thẳng a ở ngoài đường thẳng a ở ngoài đường tròn. Gọi OH là khoảng cách từ tâm O đếna và M là một điểm chuyển động trên a. Từ M kẻ hai tiếp tuyến MA,MB với đường tròn (O) , (A,B là 2 tiếp điểm). Gọi D là giao điểm của AB với OH.CMR D là điểm cố định
Trả lời :
Bn Nguyễn Tũn bảo dễ ẹt thì làm đi.
- Hok tốt !
^_^
dễ ẹc thì lm cho mk coi đi
mk ko bt lm
Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ hai tiếp tuyến MA, MB đển (O) (A, B là các tiếp điểm). Qua M kẻ cát tuyên MNP (MN MP) đến (O). Gọi K là trung điểm của NPa, Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ haib, Chứng minh tia KM là phân giác của góc
A
K
B
^
c, Gọi Q là giao điểm thứ hai của BK với (O). Chứng minh AQ song song NPd, Gọi H là giao điểm của AB...
Đọc tiếp
Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ hai tiếp tuyến MA, MB đển (O) (A, B là các tiếp điểm). Qua M kẻ cát tuyên MNP (MN < MP) đến (O). Gọi K là trung điểm của NP
a, Cho đường tròn (O) và điểm M nằm ngoài (O). Từ M kẻ hai
b, Chứng minh tia KM là phân giác của góc A K B ^
c, Gọi Q là giao điểm thứ hai của BK với (O). Chứng minh AQ song song NP
d, Gọi H là giao điểm của AB và MO. Chứng minh: MA2 = MH.MO = MN.MP
e, Chứng minh bốn điểm N, H, O, P cùng thuộc một đường tròn
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
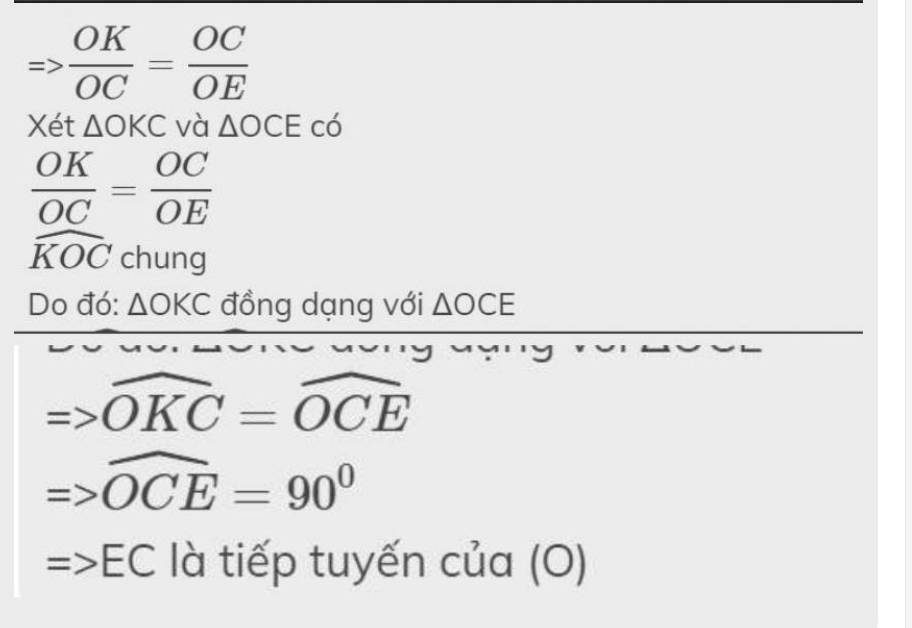
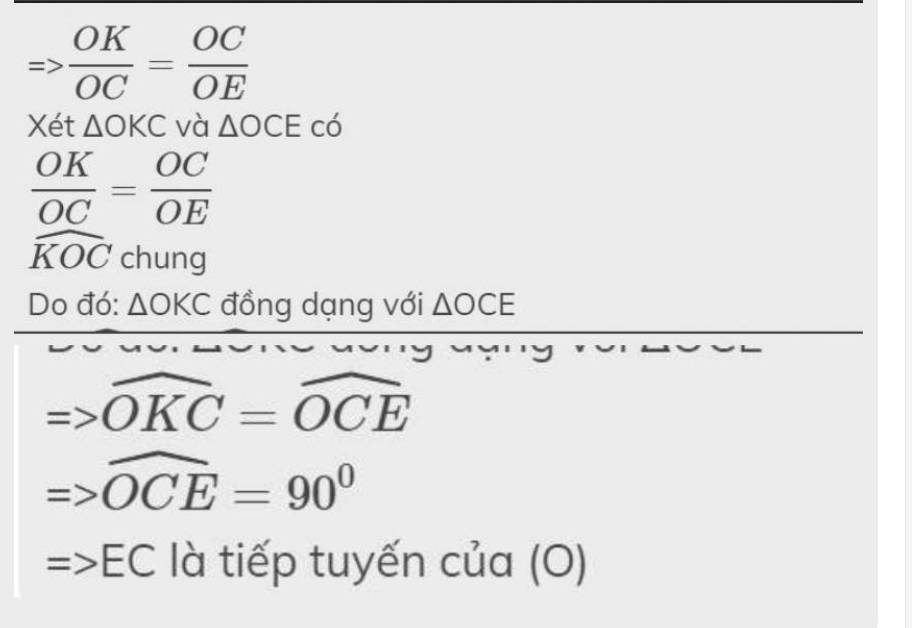
c) Chứng minh EC là tiếp tuyến của (O).
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.a) Cho OA 9 ,OM 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)b) Chứng minh MA . AE OA . ACc) Chứng minh EC là tiếp tuyến của (O). giải chi tiết giúp mik vs nhé
Đọc tiếp
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
giải chi tiết giúp mik vs nhé