Tam giác NPQ vuông tại N. NH là đường kẻ cao từ N xuống PQ. NH bằng bao nhiêu
Những câu hỏi liên quan
Cho tam giác NPQ vuông tại N (NQ<NP) gọi M là trung điểm của PQ. Từ M kẻ MD vuông góc vs NQ, ME vuông góc vs NP.
a) Chứng minh: Tứ giác NDME la hcn
b) Cm E la trung điểm cua NP và tứ giác PMDE la hbh
c) Kẻ NH vuông góc vs PQ. Cm tứ giác MHDE la hình thang cân
d) Qua N kẻ đường thẳng song song vs DH cắt DK tại K. Cm KH vuông góc vs NP.
( Ko cần giải câu a và b)
Cho tam giác ABC đều, M là điểm nằm trong tam giác. Từ M kẻ các đường thẳng song song với BC, CA, AB cắt AB, BC, CA lần lượt tại N,P,Q. Xác định vị trí của M để tam giác NPQ đều.khi đó hãy tính chu vi của tam giác NPQ theo đường cao AH của Tam giác ABC . giúp mình vs cảm ơn mọi người
Tham Khảo
3. Cho hình bình hành ABCD có AC > BD. Gọi H, K lần lượt là hình chiếu vuông góc của C trên đường thẳng AB và AD. Cmr
CH/CB=CK/CD
Tam giác CHK đồng dạng tam giác BCA
AB.AH + AD.AK= AC x AC
bài làm
![[IMG]](https://lh4.googleusercontent.com/-qw6b5CJV7g8/Ubnh5Fe6_uI/AAAAAAAAAJA/TOnMiHtG-S8/s475/unHM%252CJ%252Ctitled.GIF)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, đường cao AH. Kẻ HM vuông góc AB tại M; HN vuông góc AC tại N.
1. Chứng minh: BH = CH.
2. Chứng minh: AMN cân
3. Gọi P là giao điểm của MH với AC, Q là giao điểm của NH với AB, I là trung điểm của PQ. Chứng minh ba điểm N; H; I thẳng hàng.
1: ΔABC cân tại A
mà AH là đường cao
nen H là trung điểm của BC và AH là phân giác của góc BAC
=>HB=HC
2: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
góc MAH=góc NAH
=>ΔAMH=ΔANH
=>AM=AN
=>ΔAMN cân tại A
Đúng 0
Bình luận (0)
cho tam giác vuông abc vuông tại a kẻ đường cao am n là điểm bất kỳ thuộc cạnh bc kẻ np vuông góc với ac (p thuộc ac) kẻ nq vuông góc với ab(q thộc ab) a chứng minh an=pq b gọi i là giao điểm của an và pq chứng minh tam giác nfm là tam giác cân và góc pqm=90 độ
a: Xét tứ giác APNQ có
góc APN=góc AQN=góc PAQ=90 độ
nên APNQ là hình chữ nhật
=>AN=PQ
b: AQNP là hình chữ nhật
nên AN cắt QP tại trung điểm của mỗi đường
=>I là trung điểm chung của QP và AN
ΔAMN vuông tại M
mà MI là trung tuyến
nên MI=AN/2=PQ/2
Xét ΔMPQ có
MI là trung tuyến
MI=PQ/2
Do đó: ΔMPQ vuông tại M
Đúng 0
Bình luận (0)
Cho tam giác NPQ (N=90 độ ). PD là tia phân giác của góc P (P thuộc NQ) . Trên tia PQ lấy điểm K sao cho PN=PK
a) CM tam giác PND = PKD => DK Vuông góc PQ
b) CM PD là đường trung trực của NK
c) Kẻ NM vuông góc PQ . So sánh KM và KQ
VẼ HÌNH VS Ạ
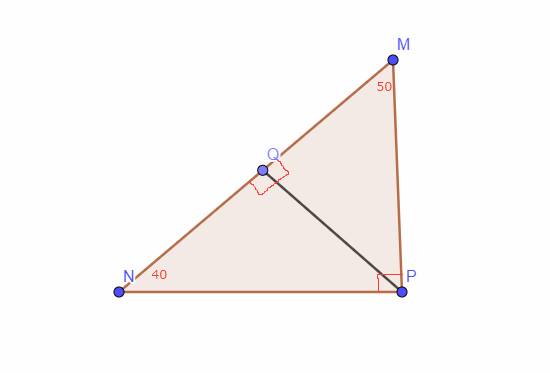
Cho tam giác MNP, có góc M = 50°, góc N = 40°, kẻ PQ vuông góc với MN. Vẽ hình và tính MPQ và NPQ
Xét Tam giác `MPQ` có:
\(\widehat{M}+\widehat{MPQ}+\widehat{MQP}=180^0\) (đli tổng 2 góc trong 1 Tam giác)
\(50^0+\widehat{MPQ}+90^0=180^0\)
`=>` \(\widehat{MPQ}=40^0\)
\(\widehat{MQP}+\widehat{NQP}=180^0\) (kề bù)
\(90^0+\widehat{NQP}=180^0\)
`=>` \(\widehat{NQP}=90^0\)
Xét Tam giác `NPQ` có:
\(\widehat{N}+\widehat{NQP}+\widehat{NPQ}=180^0\)
\(40^0+90^0+\widehat{NPQ}=180^0\)
`=>` \(\widehat{NPQ}=50^0\)
Đúng 3
Bình luận (0)
Bài 1 :Cho tam giác ABC nhọn, các đường cao BH,CK. Gọi D và E lần lượt là chân đường vuông góc kẻ từ B,C xuống đường thẳng HK. Chứng minh DK=EH
Bài 2 : Cho tam giác ABC vuông tại A, đường cao AH.Qua trung điểm M của cạnh AC, kẻ MN vuông góc với BC tại N. Gọi K là trung điểm AH. Chứng minh BK vuông góc với AN
Bài 1:
a: Ta có: ΔBKC vuông tại K
mà KM là đường trung tuyến
nên KM=BC/2(1)
Ta có: ΔBHC vuông tại H
mà HM là đường trung tuyến
nên HM=BC/2(2)
Từ (1)và (2) suy ra MH=MK
hay ΔMHK cân tại M
b: Kẻ MN vuông góc với HK
=>N là trung điểm của HK
Xét hình thang CBDE có
M là trung điểm của BC
MN//DB//EC
DO đó: N là trung điểm của DE
=>DK=HE
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Gọi M và N lần lượt là chân đường vuông góc kẻ từ H xuống AB và AC. Chứng minha)
A
H
2
A
M
.
A
B
;
b) AM,AB AN.ACc)
Δ
A
M
N
∽
Δ
A
C
B
.
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Gọi M và N lần lượt là chân đường vuông góc kẻ từ H xuống AB và AC. Chứng minh
a) A H 2 = A M . A B ;
b) AM,AB = AN.AC
c) Δ A M N ∽ Δ A C B .
Cho tam giác ABC vuông tại A có góc B=60 độ. Kẻ đường cao AH, lấy điểm D sao cho H là trung điểm của BD. Gọi I là chân đường vuông góc kẻ từ C xuống đường thẳng AD. P là giao điểm của 2 đường thẳng AH và CI. CMR: Tam giác AHC bằng tam giác CIA.