Cho hai hàm số y=2x2 và y=|mx|. Tìm m để đồ thị của hai hàm số đã cho cắt nhau tại ba điểm phân biệt là ba đỉnh của tam giác đều.

Những câu hỏi liên quan
cho p y=2x^2 và y=/mx/ tìm m để đồ thị hàm số trên cắt nhau tại 3 điểm phân biệt là ba đỉnh của tam giác
Cho hàm số
y
x
-
2
x
2
+
m
x
+
m
2
-
3
Tất cả giá trị của tham số m để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt là A. -2 m -1 B. ...
Đọc tiếp
Cho hàm số y = x - 2 x 2 + m x + m 2 - 3 Tất cả giá trị của tham số m để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt là
A. -2 < m < -1
B. - 2 < m < 2 m ≠ - 1
C. -1 < m < 2
D. - 1 < m < 2 m ≠ - 1
Chọn B.
Phương trình hoành độ giao điểm:
![]()
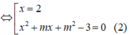
Để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt ⇔ Phương trình (1) có ba nghiệm phân biệt ⇔ Phương trình (2) có hai nghiệm phân biệt khác 2
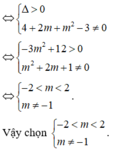
Đúng 0
Bình luận (0)
Cho hàm số
y
-
x
4
+
2
x
2
+
m
. Tất cả giá trị của tham số m để đồ thị hàm số đã cho cắt trục hoành tại ít nhất ba điểm phân biệt là A. 0 m 1 B.
-
1
m
≤
0
C. -1 m 0 D.
-
1
≤
m
0
Đọc tiếp
Cho hàm số y = - x 4 + 2 x 2 + m . Tất cả giá trị của tham số m để đồ thị hàm số đã cho cắt trục hoành tại ít nhất ba điểm phân biệt là
A. 0 < m < 1
B. - 1 < m ≤ 0
C. -1 < m < 0
D. - 1 ≤ m < 0
Chọn B.
Phương trình hoành độ giao điểm: -x4 + 2x2 + m = 0 ⇔ m = x4 - 2x2.
Đặt (C): y = x4 - 2x2 và d: y = m
Xét hàm số y = x4 - 2x2.
Ta có y' = 4x3 - 4x; y' = 0 ⇔ x = 0 ∨ x = -1 ∨ x = 1.
Bảng biến thiên:
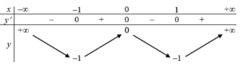
Đồ thị hàm số đã cho cắt trục hoành tại ít nhất ba điểm phân biệt khi -1 < m < 0.
Vậy chọn -1 < m < 0a
Đúng 0
Bình luận (0)
Cho hai hàm số: y=x2 -2xvà y=x3 - x2 -(m+4)x+m-1 (với m là tham số). Có bao nhiêu giá trị của ![]() để đồ thị của hai hàm số đã cho cắt nhau tại ba điểm phân biệt và ba giao điểm đó nằm trên một đường tròn bán kính bằng \(\sqrt{5}\)?
để đồ thị của hai hàm số đã cho cắt nhau tại ba điểm phân biệt và ba giao điểm đó nằm trên một đường tròn bán kính bằng \(\sqrt{5}\)?
Cho (C) là đồ thị của hàm số
y
x
-
2
x
+
1
và đường thẳng
d
:
y
m
x
+
1
. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C) A.
m
≥
0...
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 2 x + 1 và đường thẳng d : y = m x + 1 . Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A. m ≥ 0
B. m < 0
C. m ≤ 0
D. m > 0
Cho hàm số
y
x
3
-
m
x
+
1
(với m là tham số). Tìm tất cả các giá trị của m để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt. A.
m
≤
3
2
3
2
B.
m
3
2
3...
Đọc tiếp
Cho hàm số y = x 3 - m x + 1 (với m là tham số). Tìm tất cả các giá trị của m để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt.
A. m ≤ 3 2 3 2
B. m > 3 2 3 2
C. m < 3 2 3 2
D. m ≥ 3 2 3 2
Đáp án B
Phương trình hoành độ giao điểm là
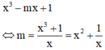
(Do x = 0 không phải là nghiệm của PT)
Xét hàm số
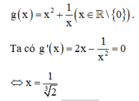
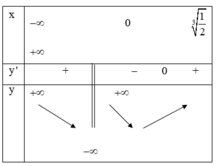
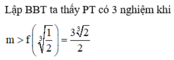
Đúng 0
Bình luận (0)
Cho hàm số:
y
x
−
1
x
2
+
m
x
+
m
. Tìm m để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt: A. ...
Đọc tiếp
Cho hàm số: y = x − 1 x 2 + m x + m . Tìm m để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt:
A. m > 4 m < 0
B. − 1 2 ≠ m < 0
C. 0 < m < 4
D. − 1 2 ≠ m < 0 m > 4
Đáp án D
Phương trình hoành độ giao điểm:
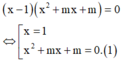
Yêu cầu bài toán <=> Phương trình (1) có hai nghiệm phân biệt khác 1
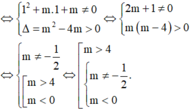
Lỗi sai:
* Một số bạn thiếu điều kiện phương trình (1) có hai nghiệm phân biệt khác 1, nên chỉ xét Δ > 0 ⇔ m > 4 m < 0 → Chọn A
Đúng 0
Bình luận (0)
Cho hàm số
x
3
+
x
2
+
m
+
1
x
+
1
và
y
2
x
+
1
. Có bao nhiêu giá trị nguyên
m
∈
-
10
;
10
để hai đồ thị của hai hàm số trên cắt nhau tại ba...
Đọc tiếp
Cho hàm số x 3 + x 2 + m + 1 x + 1 và y = 2 x + 1 . Có bao nhiêu giá trị nguyên m ∈ - 10 ; 10 để hai đồ thị của hai hàm số trên cắt nhau tại ba điểm phân biệt.
A. 9.
B. 10.
C. 1.
D. 11.
Cho (C) là đồ thị của hàm số y(x-2)/(x+1) và đường thẳng d:ymx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C) A. B. C. D.
Đọc tiếp
Cho (C) là đồ thị của hàm số y=(x-2)/(x+1) và đường thẳng d:y=mx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A.![]()
B.![]()
C.![]()
D. ![]()







