 giải hộ mình câu 10 và câu 12 nha. cảm ơn m.n
giải hộ mình câu 10 và câu 12 nha. cảm ơn m.n

Những câu hỏi liên quan
-7/12 + 11/8 - 5/9
Giúp mình nha, mình còn nhiều câu sau tương tự thế này nữa. Mng giải hộ mình để mình tự mò mấy câu sau nha, cảm ơn mng nhiều
Giải :
-7/12 + 11/8 - 5/9
= 17/72
Học tốt !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
lấy tổng của 7/12 và 11/8 trừ đi 5/9 bằng 17/72
#hok tốt
Đáp số: \(\frac{17}{72}\)
~~~Hok tốt~~~
Xem thêm câu trả lời
Giúp mình giải những câu này với ạ (có giải thích nữa nha). Cảm ơn m.n nhiều!
Đọc tiếp
Giúp mình giải những câu này với ạ (có giải thích nữa nha). Cảm ơn m.n nhiều!

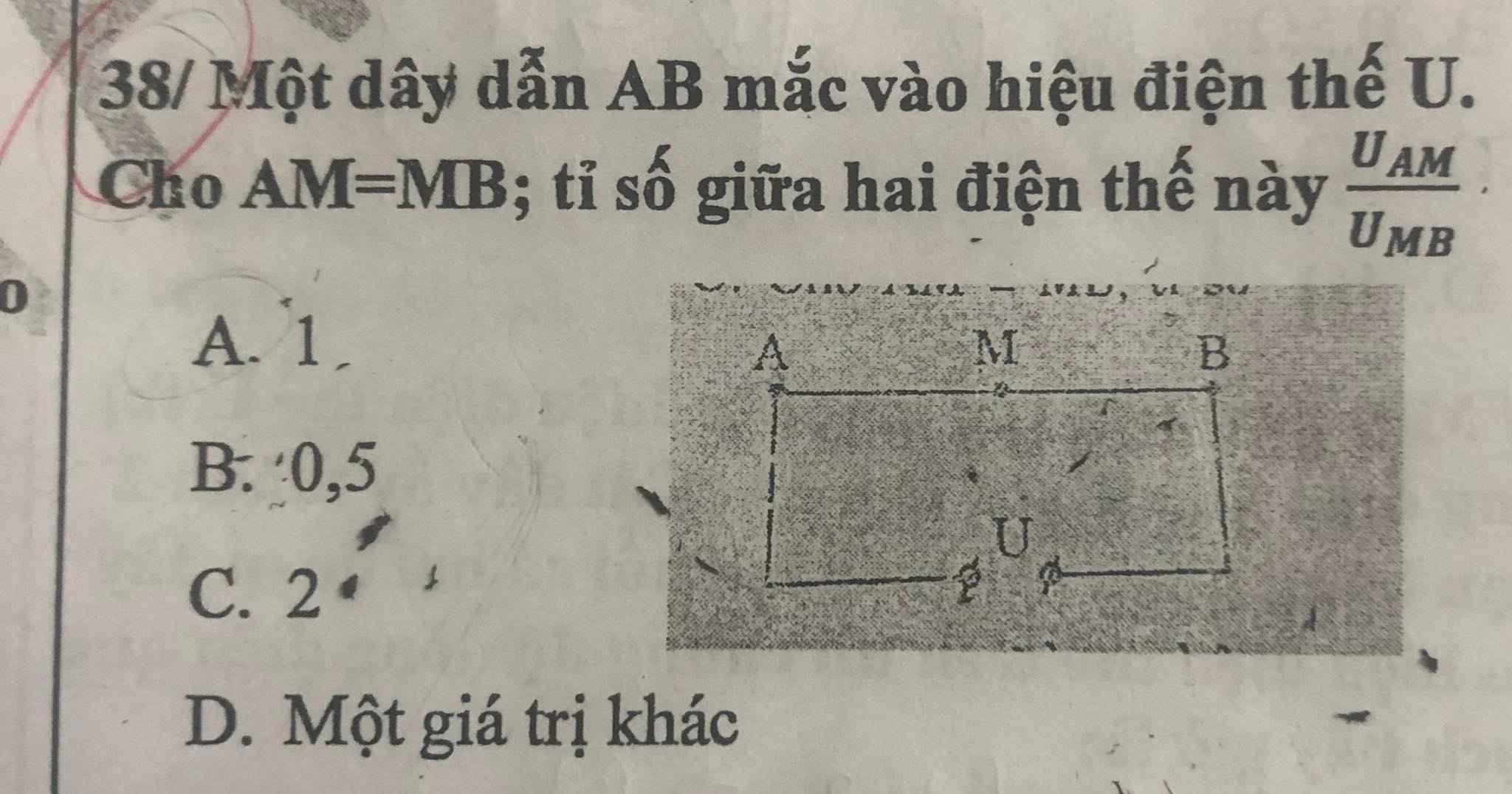
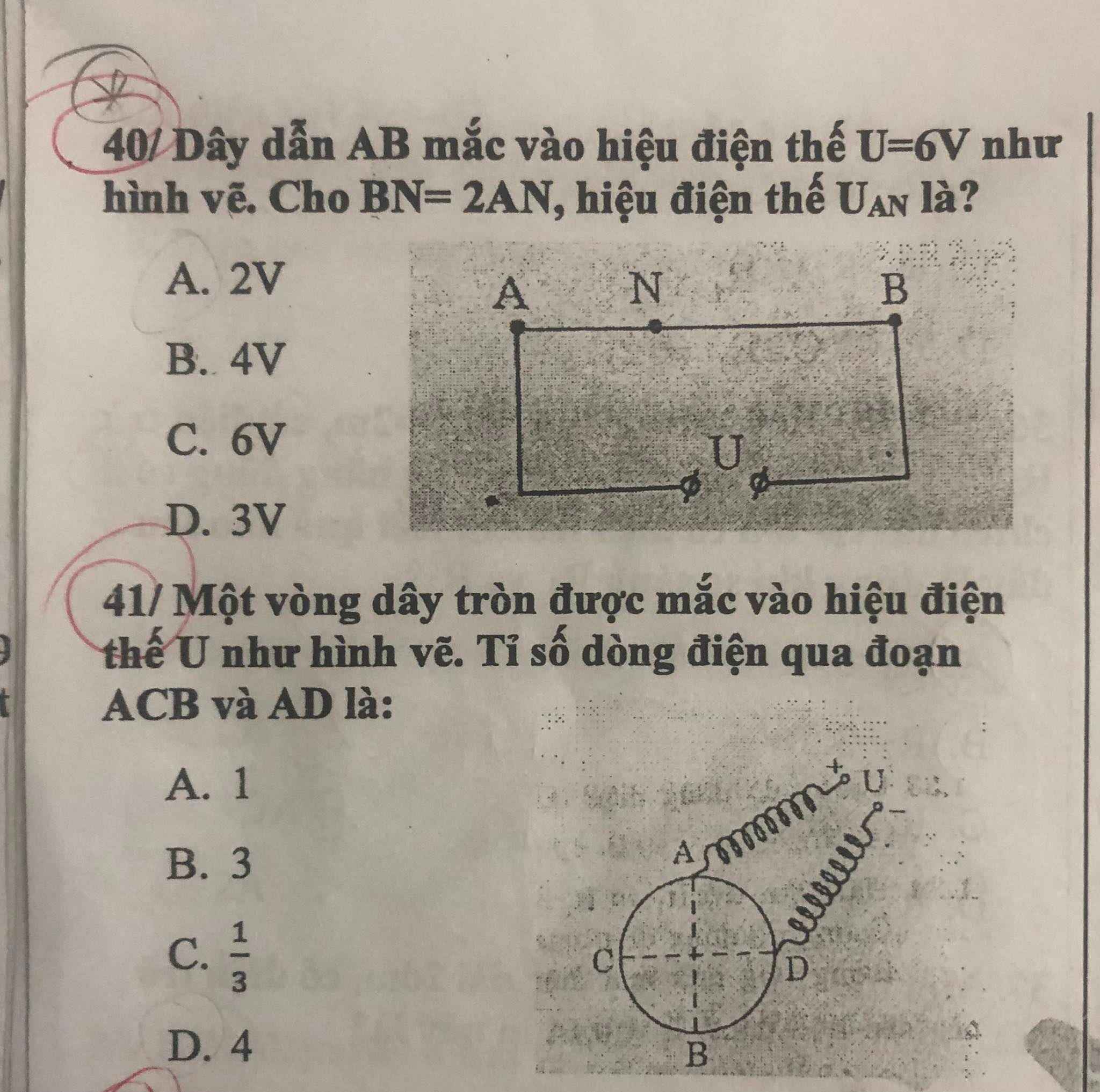
Ai giải hộ mình câu 10 và 11 với! Mik cảm ơn nhiều ạ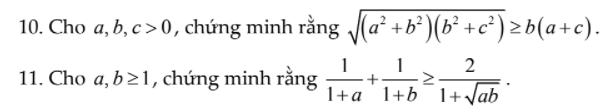 !
!
10. Câu này chứng minh BĐT BSC:
\(\sqrt{\left(a^2+b^2\right)\left(b^2+c^2\right)}\ge\sqrt{\left(ab+bc\right)^2}=b\left(a+c\right)\)
Đúng 1
Bình luận (0)
11.
Ta có: \(\dfrac{1}{1+a}+\dfrac{1}{1+b}-\dfrac{2}{1+\sqrt{ab}}\)
\(=\dfrac{\left(1+b\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{\left(1+a\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2\left(1+a\right)\left(1+b\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{1+b+\sqrt{ab}+b\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{1+a+\sqrt{ab}+a\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2+2a+2b+2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{-a-b+2\sqrt{ab}+a\sqrt{ab}+b\sqrt{ab}-2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2\left(\sqrt{ab}-1\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\ge0\forall x,y\ge1\)
Đẳng thức xảy ra khi \(a=b=1\)
Đúng 0
Bình luận (0)
Ai giải hộ mình câu 10 và 11 với! Mik cảm ơn rất nhiều ạ.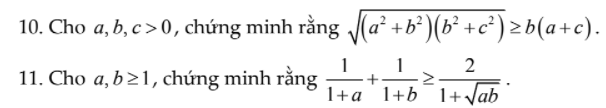
dùng phương pháp hình học cm câu a
đặt BH =a , HC =c kẻ HA =b
theo định lí py ta go ta có
AB=a2+b2;AC=b2+c2;BC=a+b
dễ thấy AB.AC\(\ge\) 2SABC=BC.AH
(a2+b2).(b2+c2)\(\ge\)b.(a+c)
Đúng 0
Bình luận (0)
các bạn giải hộ mình câu 5 nha mình cảm ơn nhiều
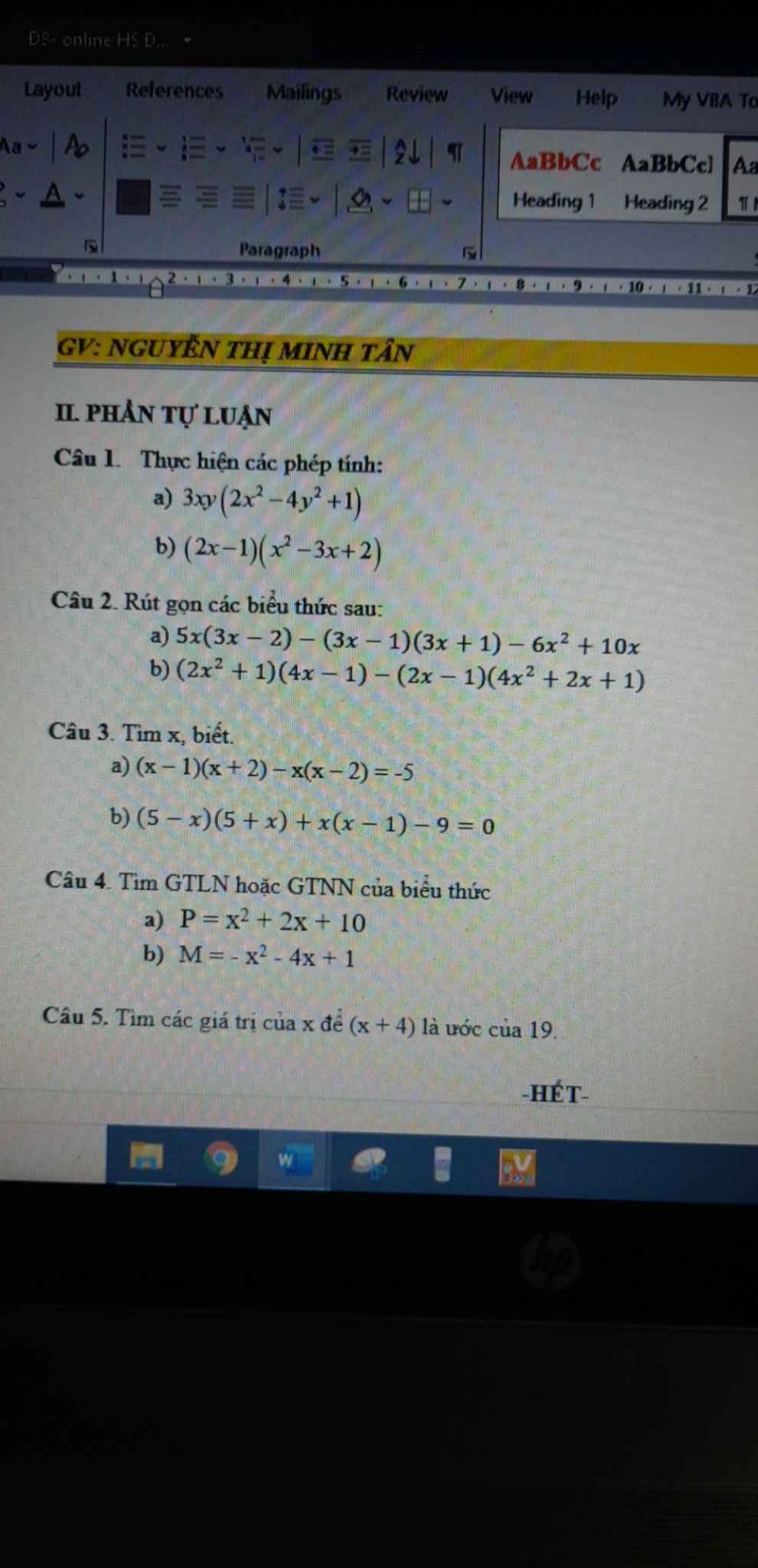
Ai giải hộ mình câu 10 và 11 với! Mik đang cần ạ, cảm ơn nhiều!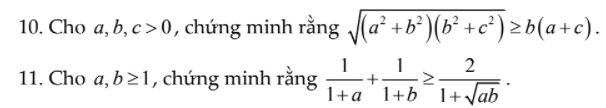
12/16<.../22<13/16
Mn giải hộ mình câu này với ạ, mình cảm ơn nhiều.
\(\dfrac{12}{16}=\dfrac{132}{176}\\ \dfrac{13}{16}=\dfrac{143}{176}\\ Ta.có:\dfrac{16}{22}< \dfrac{132}{176}< \dfrac{17}{22}< \dfrac{143}{176}< \dfrac{18}{22}\\ Vậy:Chọn.số.17\)
Đúng 1
Bình luận (0)
làm nhanh mình tik nha , cảm ơn trc ạ
giải thích ra nhe , đừng chọn đại câu hộ mình
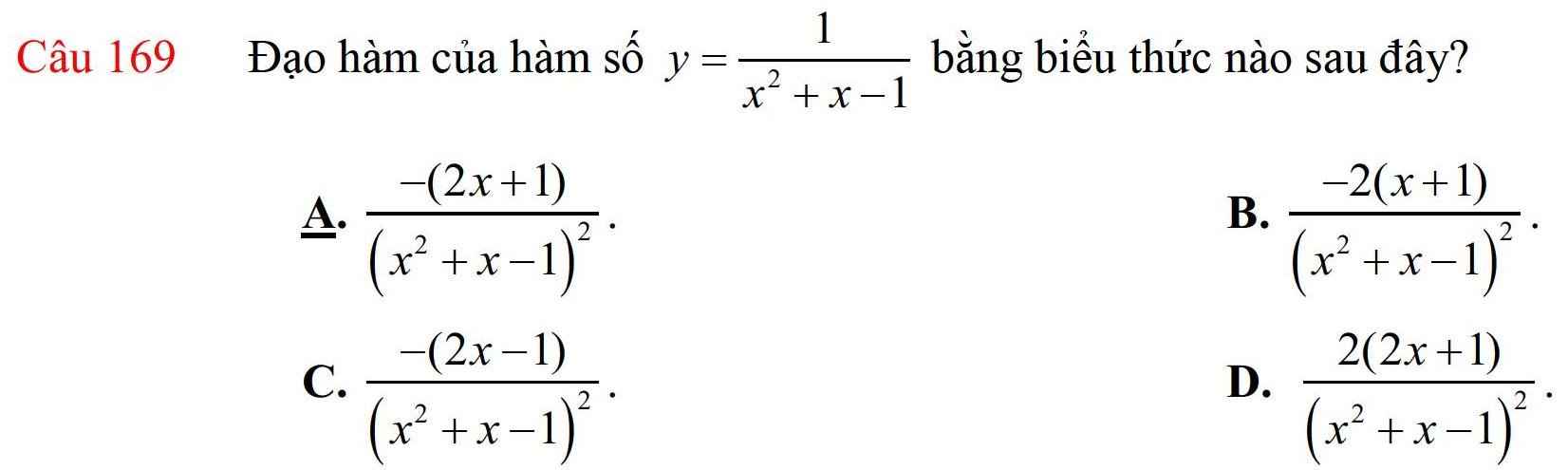
Áp dụng công thức \(\left(\dfrac{1}{v}\right)'=\dfrac{-v'}{v^2}\)
Ta có \(y'=\dfrac{-\left(x^2+x-1\right)'}{\left(x^2+x-1\right)^2}=-\dfrac{\left(2x+1\right)}{\left(x^2+x-1\right)^2}\)
Đúng 0
Bình luận (1)
M.n ơi m.n giải giúp mình câu d,đ với ạ
Mình đang cần gấp ạ
Mình cảm ơn
















