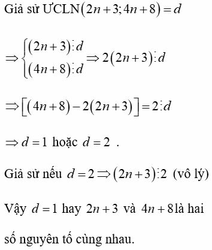gọi a là ước chung lớn nhất của 2n+1 và 3n+2

do đó a phải là ước của \(2\left(3n+2\right)-3\left(2n+1\right)=1\) do đó a=1

hay 2n+1 và 3n+2 là hai số nguyên tố cùng nhau.

b.gọi b là ước chung lớn nhất của 2n+3 và 4n+5

do đó b phải là ước của \(2\left(2n+3\right)-\left(4n+5\right)=1\)do đó b=1

hay 2n+3 và 4n+5 là hai số nguyên tố cùng nhau

chtt

chtt

Gọi ƯCLN(2n + 3; 4n + 8) là d

=> 2n + 3 chia hết cho d => 2(2n + 3) chia hết cho d

     4n + 8 chia hết cho d

Từ 2 điều trên => (4n + 8) - 2(2n + 3) chia hết cho d

=> 4n + 8 - 4n - 6 chia hết cho d

=> (4n - 4n) + (8 - 6) chia hết cho d

=> 2 chia hết cho d

=> d thuộc {1; 2}

Ta thấy 2n + 3 là lẻ mà 2n + 3 chia hết cho d nên d lẻ

=> d = 1

=> ƯCLN(2n + 3; 4n + 8) = 1

Vậy...

Gọi ƯCLN(2n+3;4n+8)=d

Ta có: 2n+3 chia hết cho d=>2(2n+3) chia hết cho d=>4n+6 chia hết cho d

=>4n+8-(4n+6) chia hết cho d hay 2 chia hết cho d

mà 2n+3 lẻ, 4n+8 chẵn nên d=1

Vậy 2n+3 và 4n+8 là 2 số nguyên tố cùng nhau

Gọi d > 0 là ước số chung của 2n+3 và 4n + 8

⇒ d ∈ Ư [2﴾2n + 3﴿ = 4n + 6]

﴾4n + 8﴿ ‐ ﴾4n + 6﴿ = 2

⇒ d ∈ Ư﴾2﴿ ⇒ d ∈ {1,2}

d = 2 không là ước số của số lẻ 2n+3

⇒ d = 1

vậy 2n+3 và 4n + 8 nguyên tố cùng nhau

Goi d là ƯCLN ( 2n + 3 ; 4n + 8 )

\(\Rightarrow\) 2n + 3 và 4n + 8 chia hết cho d

\(\Rightarrow\) 2 . ( 2n + 3 ) chia hết cho d

          1 . ( 4n + 8 ) chia hết cho d

\(\Rightarrow\) 4n + 6 chia hết cho d 

           4n + 8 chia hết cho d

\(\Rightarrow\) 4n + 8 - ( 4n + 6 ) chia hết cho d

          4n + 8 - ( 4n - 6 ) chia hết cho d

Suy ra 2 chia hết cho d .

        d € Ư ( 2 ) = { 1 ; 2 }

Mà 2n + 3 không chia hết cho 2 . Suy ra d = 1

\(\Rightarrow\) ƯCLN ( 2n + 3 ; 3n + 4 ) = 1

Vậy 2n + 3 và 3n + 4 là 2 số nguyên tố cùng nhau .

4n+8=2(2n+4)

2n+3,2n+4 ng tố cùng nhau 2 stn liên tiếp

 k mình nha

sai đề

bạn ơi hình như nhầm đề hai số này ko thể nguyên tố cùng nhau

nếu là đề đúng thì sẽ làm như sau(sửa 4n+3 thành 4n+4)

gọi UCLN của 2n+3 và 4n +4 là D

2n+3 và 4n+4 chia hết cho D

ta có thể viết thành 4.(2n+3)và 2.(4n+4)chia hết cho D

và ta có 8n+6 và 8n+8 chia hết cho D

và ta có kq là 2 chia hết cho D

vì hai số nguyên tố cùng nhau sẽ có UCLN =1 nên => D =1

ta sẽ lấy 8n+8-8n+6=2

Tham Khảo:

Giả sử: \(UCLN\left(2n+3;4n+8\right)=d\)

=> \(\left\{{}\begin{matrix}2n+3⋮d\\4n+8⋮d\end{matrix}\right.\) => \(\left\{{}\begin{matrix}4n+6⋮d\\4n+8⋮d\end{matrix}\right.\)

=> \(2⋮d\) => \(\left[{}\begin{matrix}d=1\\d=2\end{matrix}\right.\)

Có 2n+3 là số lẻ => \(2n+3⋮̸2\)

=> d = 1

=> đpcm

Giả sử ƯCLN(2n+3 ;4n+8) = d

2 n + 3 ⋮ d 4 n + 8 ⋮ d ⇒ 2 2 n + 3 ⋮ d

=>  4 n + 8 - 2 2 n + 3 = 2 ⋮ d

=>d = 1 hoặc d = 2 .

Giả sử nếu d = 2 => (2n+3) ⋮ 2 (vô lý)

Vậy d = 1 hay 2n+3 và 4n+8 là hai số nguyên tố cùng nhau