Cho tam giác ABC có AB = 9 cm ; AC = 12 cm và BC = 16 cm. Các đường phân giác AD, BE, CF cắt nhau ở O. Tính giá trị của \(\dfrac{OA}{OD}.\dfrac{OB}{OE}.\dfrac{OC}{OF}\)
Giúp em với thầy cô ơi em đang gấp lắm ạ
Hai tam giác AEF và ABF có chung đường cao hạ từ F nên ta có \(\frac{S_{AEF}}{S_{ABF}}=\frac{AE}{AB}=\frac{4}{6}=\frac{2}{3}\)(1)
Hai tam giác ABF và ABC có chung đường cao hạ từ B nên ta có \(\frac{S_{ABF}}{S_{ABC}}=\frac{AF}{AC}=\frac{4}{9}\)(2)
Từ (1) và (2) \(\Rightarrow\frac{S_{AEF}}{S_{ABF}}.\frac{S_{ABF}}{S_{ABC}}=\frac{2}{3}.\frac{4}{9}\)\(\Rightarrow\frac{S_{AEF}}{S_{ABC}}=\frac{8}{27}\)\(\Rightarrow S_{AEF}=\frac{8}{27}S_{ABC}=\frac{8}{27}.27=8\left(cm^2\right)\)
Vậy \(S_{AEF}=8cm^2\)
Bạn vào thống kê hỏi đáp của mình xem câu trả lời nhé. Nó chưa duyệt lên.
Cho tam giác ABC vuông tại A có AB = 9 cm, AC = 12 cm. Gọi I là tâm đường tròn nội tiếp tam giác ABC, G là trọng tâm của tam giác ABC. Tính độ dài IG
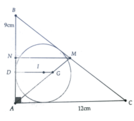
Gọi M là trung điểm của BC
Ta tính được AG = 2 3 AM = 10cm
Gọi N là trung điểm của AB => MN//AC, MN ⊥ AB
D,I,G thẳng hàng
<=> A G A M = A D A N = 2 3 <=> A D 2 A N = 1 3 <=> A D A B = 1 3
Ta có AD = r nội tiếp = A B + A C - B C 2 <=> A B 3 = A B + A C - B C 2
<=> AB+3AC = 3BC = A B 2 + A C 2
<=> 3AC = 4AB (đpcm)
Áp dụng kết quả trên ta có: AD = A B + A C - B C 2 = 3cm
=> ID = DA = 3cm => IG = DG – ID = 1cm
Cho tam giác ABC có AB=6,AC=5,BC=9. Trên tia đối của AB lấy D sao cho AD=AC. a) Cm tam ADC đồng dạng với tam giác ABC. b) Tính CD. c) Cm góc BAC=2 lần góc ACD
Sửa đề: AC=7,5
a: Sửa đề: ΔABC đồng dạng với ΔCBD
Xét ΔABC và ΔCBD có
BA/BC=CB/BD
góc B chung
=>ΔABC đồng dạng với ΔCBD
b: ΔABC đồng dạng với ΔCBD
=>AC/CD=AB/CB
=>7,5/CD=6/9=2/3
=>CD=11,25(cm)
1. Cho tam giác ABC vuông tại A có AB = 9 cm , BC = 15 cm , AH là đường C10 ( H thuộc cạnh BC ) . Tính BH , CH , AC và AH ,
2. Cho tam giác ABC vuông tại A có AC = 5 cm , AB = 4 cm . Tính : a ) Cạnh huyền BC . b ) Hình chiếu của AB và AC trên cạnh huyền . c ) Đường cao AH .
3. Cho tam giác ABC vuông tại A có BC = 40 cm , AC = 36 cm . Tính AB , BH , CH và AH ,
4. Cho tam giác ABC vuông tại A có BC = 24 cm . Tính AB , AC , cho biết 2 AB = -AC .
5. Cho tam giác ABC vuông tại A có AH là đường cao . BH = 10 cm , CH = 42 cm . Tính BC , AH , AB và AC ,
6. Cho đường tròn tâm O bán kính R = 10 cm . A , B là hai điểm trên đường tròn ( O ) và I là trung điểm của đoạn thẳng AB . a ) Tính AB nếu OI = 7 cm . b ) Tính OI nếu AB = 14 cm .
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=15^2-9^2=144\)
hay AC=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\\CH=\dfrac{12^2}{15}=\dfrac{144}{15}=9,6\left(cm\right)\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AH^2+HB^2=AB^2\)
\(\Leftrightarrow AH^2=9^2-5.4^2=51,84\)
hay AH=7,2(cm)
1. Cho tam giác ABC vuông tại A có AB = 9 cm , BC = 15 cm , AH là đường C10 ( H thuộc cạnh BC ) . Tính BH , CH , AC và AH ,
2. Cho tam giác ABC vuông tại A có AC = 5 cm , AB = 4 cm . Tính : a ) Cạnh huyền BC . b ) Hình chiếu của AB và AC trên cạnh huyền . c ) Đường cao AH .
3. Cho tam giác ABC vuông tại A có BC = 40 cm , AC = 36 cm . Tính AB , BH , CH và AH ,
4. Cho tam giác ABC vuông tại A có BC = 24 cm . Tính AB , AC , cho biết 2 AB = -AC .
5. Cho tam giác ABC vuông tại A có AH là đường cao . BH = 10 cm , CH = 42 cm . Tính BC , AH , AB và AC ,
6. Cho đường tròn tâm O bán kính R = 10 cm . A , B là hai điểm trên đường tròn ( O ) và I là trung điểm của đoạn thẳng AB . a ) Tính AB nếu OI = 7 cm . b ) Tính OI nếu AB = 14 cm .
Cho tam giác ABC vuông tại A ,có phân giác BD, biết AB = 9 cm, BC = 15 cm .Tính AC, DC, DA?
Theo định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=12cm\)
Vì BD là pg \(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Rightarrow\dfrac{DC}{BC}=\dfrac{AD}{AB}\)
Theo tc dãy tỉ số bằng nhau ta có
\(\dfrac{DC}{BC}=\dfrac{AD}{AB}=\dfrac{12}{24}=\dfrac{1}{2}\Rightarrow DC=\dfrac{15}{2}cm;DA=\dfrac{9}{2}cm\)
cho tam giác ABC có AB=6 cm, AC=9 cm. các điểm D, E theo thứ tự thuộc các cạnh AB, AC sao cho BD=4 cm, CE=6 cm.
1)chứng minh rằng tam giác ADE đồng dạng tam giác ABC, tính tỉ số đồng dạng.
2)kẻ EK//AB(K thuộc BC) chứng minh rằng tam giác ade đồng dạng tam giác ekc
3) tính chu vi tam giác EKC biết BC = 12 cm
cho tam giác ABC bằng tam giác DEF có BC = 12 cm ,AB /AC bằng 8 / 9 và AB + AC = 17.Tính độ dài các cạnh của tam giác DEF
ai bít cho đáp an vs
AB=17*8/17=8cm
AC=17-8=9cm
DE=AB=8cm; BC=EF=12cm; AC=DF=9cm
cho tam giác abc có ab =6cm,ac=9 cm gọi e,f lần lượt là các điểm trên ab ,ac .sao cho ae =4cm,af=6cm.a)chứng minh tam giác aef đồng dạng với tam giác abc b) cho EF = 3cm hãy tính BC
Ta có AB/AE = AC/AF
<=> 6/4=9/6=3/2
AEF và ABC chung góc A
=> AEF và ABC đồng dạng "cạnh góc cạnh "
b) BC =3x3/2=4,5cm
`a)` Ta có: `(AE)/(AB) = 4/6 = 2/3`
`(AF)/(AC) = 6/9 = 2/3`
`=> (AE)/(AB) = (AF)/(AC)`
Xét `ΔAEF` và `ΔABC` có:
`hat{A}` chung
`(AE)/(AB) = (AF)/(AC)`
`=> ΔAEF ∼ ΔABC (c - g - c) ` (đpcm)
`b) ` Theo `a) ΔAEF ∼ ΔABC `
`=> (EF)/(BC) = (AF)/(AC)`
`=> 3/(BC) = 2/3`
`=> BC = 3 : 2/3 = 9/2`
Vậy `BC = 9/2cm`
cho tam giác ABC, có AB = 9 cm, AC =12 cm, BC = 15cm, CE là phân giác, trên cạnh AC, BC lấy F và K sao cho À = BK = 3 cm.
a) tính AE
b) CMR: tam giác AEF đồng dạng với tam giác ABC
c) CMR: tam giác AEF đồng dạng với tam giác KBE
Xem cách hack VIP OLM siêu dễ chỉ 10p xong tại đây: https://www.youtube.com/watch?v=zYcnHqUcGZE