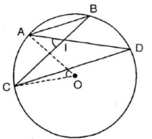
Cho đường tròn tâm O có hai dây cung AB và CD song song. Chứng minh cung AC = cung BD

Những câu hỏi liên quan
Giả sử AB là một dây cung của đường tròn (O). Trên cung nhỏ AB lấy các điểm C và D sao cho A C ⏜ = B D ⏜ . Chứng minh AB và CD song song
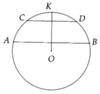
Ta lấy K là điểm chính giữa cung nhỏ A B ⏜
Ta chứng minh được C K ⏜ = K D ⏜
Từ đó ta có OK ⊥ CD, OK ⊥ AB => CD//AB
Đúng 1
Bình luận (0)
cho đường tròn tâm O đường kính AB. Từ A và B vẽ hai dây cung AC và BD song song với nhau . So sánh hai cung nhỏ AC và BD
Xét (O) có
AC là dây
BD là dây
AC//BD
Do đó: AC=BD
Đúng 1
Bình luận (0)
cho đường tròn tâm O đường kính Ab. Từ A và B vẽ hai dây cung AC và BD song song với nhau .So sánh hai cung nhỏ AC và BD
B1: Chứng minh rằng trong một đường tròn, hai dây cung không cắt nhau AB và CD là song song khi và chỉ khi hai cung AC và BD bằng nhau B2: Cho hai đường tròn tiếp xúc trong tại điểm A và BC là 1 dây của đường tròn lớn đường tiếp xúc với đường tròn nhỏ tại điểm D. Chứng minh rằng AD là phân giác của góc BAC
Cho đường tròn tâm O đường kính AB. Từ A và Bvẽ hai dây AC và BD song song với nhau. So sánh hai cung nhỏ A C ⏜ và B D ⏜
Ta chứng minh được ∆ABC = ∆BDA từ đó suy ra A C ⏜ = B D ⏜
Đúng 0
Bình luận (0)
Cho đường tròn (O;R) và dây cung AB cố định không đi qua tâm O; C và D là hai điểm di động trên cung lớn AB sao cho AD và BC luôn song song với nhau. Gọi M là giao điểm của AC và BD . Chứng minh rằng: 1) , suy ra AOMB là tứ giác nội tiếp. 2) 3) Đường thẳng d đi qua M và song song với AD luôn đi qua một điểm cố định.
Đọc tiếp
Cho đường tròn (O;R) và dây cung AB cố định không đi qua tâm O; C và D là hai điểm di động trên cung lớn AB sao cho AD và BC luôn song song với nhau. Gọi M là giao điểm của AC và BD . Chứng minh rằng:
1) ![]() , suy ra AOMB là tứ giác nội tiếp.
, suy ra AOMB là tứ giác nội tiếp.
2) ![]()
3) Đường thẳng d đi qua M và song song với AD luôn đi qua một điểm cố định.
Cho đường tròn tâm O có 2 dây AB // CD . Chứng minh cung AC = cung BD.
Cho đường tròn (O) đường kính AB và một cung AC có số đo nhỏ hơn 90 0 . Vẽ dây CD vuông góc với AB và dây DE song song với AB. Chứng minh AC = BE

Ta chứng minh A D ^ = B E ^ , mà CD ⊥ AB nên từ đó suy ra
* Cách khác:Chứng minh A O C ^ = B O E ^ => ĐPCM
Đúng 0
Bình luận (0)
Cho đường tròn (O) đường kính AC và điểm B trên nửa đường tròn sao cho sđ cung BC =60°. Qua B kẻ dây BD vuông góc AC, qua D kẻ dây DF song song AC.
a, Tính số đo các cung CD, AB, FD
b, Tìm tiếp tuyến của (O) song song với AB
a: Xét (O) có
ΔBAC nội tiếp
AC là đường kính
Do đó: ΔBAC vuông tại B
Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{BAC}=\dfrac{1}{2}\cdot sđ\stackrel\frown{BC}=\dfrac{1}{2}\cdot60^0=30^0\)
Gọi H là giao điểm của BD với AC
BD\(\perp\)AC nên BD\(\perp\)AC tại H
ΔOBD cân tại O
mà OH là đường cao
nên H là trung điểm của BD
Xét ΔCBD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCBD cân tại C
=>CB=CD
Xét ΔCOD và ΔCOB có
CD=CB
OD=OB
CO chung
Do đó: ΔCOD=ΔCOB
=>\(\widehat{COD}=\widehat{COB}\)
=>\(sđ\stackrel\frown{CB}=sđ\stackrel\frown{CD}=60^0\)
Xét ΔBAC vuông tại B có \(\widehat{BAC}+\widehat{BCA}=90^0\)
=>\(\widehat{BCA}+30^0=90^0\)
=>\(\widehat{BCA}=60^0\)
Xét (O) có
\(\widehat{BCA}\) là góc nội tiếp chắn cung AB
Do đó: \(\widehat{BCA}=\dfrac{1}{2}\cdot sđ\stackrel\frown{AB}\)
=>\(sđ\stackrel\frown{AB}=2\cdot\widehat{BCA}=120^0\)
DF//AC
DB\(\perp\)AC
Do đó: DF\(\perp\)DB
=>ΔDFB vuông tại D
ΔDFB vuông tại D
nên ΔDFB nội tiếp đường tròn đường kính BF
mà ΔDFB nội tiếp (O)
nên O là trung điểm của BF
=>OA//DF
=>\(\widehat{BFD}=\widehat{BOH}=\widehat{BOC}\)(hai góc đồng vị)
=>\(\widehat{BFD}=60^0\)
ΔBDF vuông tại D
=>\(\widehat{BFD}+\widehat{FBD}=90^0\)
=>\(\widehat{FBD}+60^0=90^0\)
=>\(\widehat{FBD}=30^0\)
Xét (O) có
\(\widehat{FBD}\) là góc nội tiếp chắn cung FD
Do đó: \(\widehat{FBD}=\dfrac{1}{2}\cdot sđ\stackrel\frown{FD}\)
=>\(sđ\stackrel\frown{FD}=2\cdot\widehat{FBD}=2\cdot\)30=60 độ
Đúng 1
Bình luận (0)
Cho đường tròn (O) và hai dây cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD); AD cắt BC tại I. Chứng minh:
AOC ^ = AIC ^