Thần điểu thập tam tứ đại đoàn
Tiểu kim tứ sắc phận đa đoan
Thiên nhãn quang linh ngự đỉnh tháp
Tự họa tề lai khúc khải hoàn
Dịch thơ cho mình!
Cảm nghĩ khổ thơ sau :
“Dưa La, cà Láng, nem Báng, tương Bần, nước mắm Vạn Vân, cá rô đầm Sét
Vải Quang, húng Láng, ngổ Đầm, cá rô đầm Sét, sâm cầm hồ Tây.
Ổi Định Công, nhãn lồng làng Quang, vàng làng Tó, kéo vó Xóm Văn
Bằng vải, Bằng dưa, Linh cua, Tứ bún
Rau cải làng Tiếu chấm nước điếu cũng ngon
Cam canh, hồng Diến, cốm Vòng
Bán mít chợ Đông, bán hồng chợ Tây, bán mây chợ Huyện, bán quyến chợ Đào
Diêm quả đào, thuốc lào làng Nhót
Lĩnh Bưởi, lụa La, thêu hoa Ngũ Xã
Cỗ Dương Đanh, hành làng Nội, hội làng Lam, tàn làng Quán, hương án làng Đề”
Khổ thơ nói về các đặc sản, các món ngon ở các vùng miền và cũng là đặc điểm để nhận dạng các vùng miền đó.
Ở một loài thực vật, xét 2 cặp gen Aa, Bb phân li độc lập, mỗi gen quy định một tính trạng, alen trội là trội hoàn toàn. Sử dụng cônsixin tác động lên 1 đỉnh sinh trưởng của cây có kiểu gen aaBb để gây tứ bội. Cây này tự thụ phấn, thu được F1. Biết rằng cơ thể tứ bội giảm phân chỉ sinh ra giao tử lưỡng bội và thể tam bội không có khả năng sinh sản hữu tính. Có bao nhiêu phát biểu sau đây đúng?
I. Thể tam bội ở F1 có tối đa 4 loại kiểu gen.
II. Cho các cây tứ bội F1 lai với nhau, có tối đa 15 sơ đồ lai.
III. Cho các cây lưỡng bội F1 lai với nhau, có tối đa 6 sơ đồ lai.
IV. Cho F1 tự thụ phấn, có tối đa 8 sơ đồ lai
A. 1.
B. 2
C. 3.
D. 4.
Đáp án D
Cả 4 phát biểu trên đều đúng.
I đúng. Tứ bội lai với lưỡng bội
(aaaaBBbb × aaBb) thì có số loại
KG = 1 × 4 = 4.
II đúng. Tứ bội lai với nhau
(aaaaBBbb × aaaaBBbb)
thì có số loại kiểu gen = 1 × 5 = 5.
Tứ bội F1 có 5 kiểu gen.
→ Khi 5 kiểu gen này lai với nhau
thì có số sơ đồ lai
= 5 × (5+1)/2 = 15.
III đúng. Lưỡng bội lai với nhau
(aaBb × aaBb) thì có số loại
kiểu gen = 1 × 3 = 3.
→ Số sơ đồ lai = 3 × (3+1)/2 = 6.
IV đúng. F1 có 5 kiểu gen tứ bội,
3 kiểu gen lưỡng bội.
→ Có 8 kiểu gen. Các kiểu gen này
tự thụ phấn thì có số sơ đồ lai
= 8 sơ đồ lai.
(Thể tam bội không có khả năng sinh sản).
Ở một loài thực vật, xét 2 cặp gen Aa, Bb phân li độc lập, mỗi gen quy định một tính trạng, alen trội là trội hoàn toàn. Sử dụng cônsixin tác động lên 1 đỉnh sinh trưởng của cây có kiểu gen aaBb để gây tứ bội. Cây này tự thụ phấn, thu được F1. Biết rằng cơ thể tứ bội giảm phân chỉ sinh ra giao tử lưỡng bội và thể tam bội không có khả năng sinh sản hữu tính. Có bao nhiêu phát biểu sau đây đúng?
I. Thể tam bội ở F1 có tối đa 4 loại kiểu gen.
II. Cho các cây tứ bội F1 lai với nhau, có tối đa 15 sơ đồ lai.
III. Cho các cây lưỡng bội F1 lai với nhau, có tối đa 6 sơ đồ lai.
IV. Cho F1 tự thụ phấn, có tối đa 8 sơ đồ lai.
A. 1
B. 2
C. 3
D. 4
Đáp án D
Cả 4 phát biểu trên đều đúng. → Đáp án D.
I đúng. Tứ bội lai với lưỡng bội (aaaaBBbb × aaBb) thì có số loại KG = 1 × 4 = 4.
II đúng. Tứ bội lai với nhau (aaaaBBbb × aaaaBBbb) thì có số loại kiểu gen = 1 × 5 = 5.
Tứ bội F1 có 5 kiểu gen. → Khi 5 kiểu gen này lai với nhau thì có số sơ đồ lai = 5 × (5+1)/2 = 15.
III đúng. Lưỡng bội lai với nhau (aaBb × aaBb) thì có số loại kiểu gen = 1 × 3 = 3.
→ Số sơ đồ lai = 3 × (3+1)/2 = 6.
IV đúng. F1 có 5 kiểu gen tứ bội, 3 kiểu gen lưỡng bội. → Có 8 kiểu gen. Các kiểu gen này tự thụ phấn thì có số sơ đồ lai = 8 sơ đồ lai. (Thể tam bội không có khả năng sinh sản)
viết bài văn thuyết minh về chùa sắc tứ khải đoan
Nhất chích, nhất chích hựu nhất chích
Tam tứ, ngũ lục, thất bát chích
Phượng hoàng hà thiểu, điểu hà đa
Thực tận nhân gian thiên vạn thạch.
Tam nhân đồng hành thất thập hy,
Ngũ thụ mai hoa trấp nhất chi,
Thất tử đào viên thu bán nguyệt,
Cọng (cộng) trừ bách linh ngũ, định vi kỳ.
Song phi đồng hành thập ngũ hy,
Tam thụ mai hoa hữu thập chi,
Ngũ tử đào viên du lục nguyệt,
Cọng, trừ tam thập định vi kỳ.
Mặt em phương tượng chữ điền,
Da em thì trắng, áo đen mặc ngoài.
Lòng em có đất, có trời,
Có câu nhân nghĩa, có lời hiếu trung.
Dù khi quân tử có dùng,
Thì em sẽ ngỏ tấm lòng cho xem
Ai đúng thì mình tích cho
Đây là chỗ để học Toán. Bạn ko nên đăng các câu hỏi ko liên quan đến Toán
Đây là đố vui ko phải là toán nhé bạn
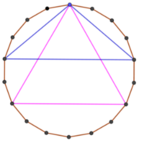
Cho đa giác đều 20 đỉnh. Lấy ngẫu nhiên 4 đỉnh trong các đỉnh của đa giác. Tính xác suất để 4 đỉnh lấy được tạo thành tứ giác có 2 góc ở 2 đỉnh kề chung một cạnh của tứ giác là 2 góc tù.
A . 112 323
B . 14 323
C . 14 19
D . 16 19
Chọn D
Số cách chọn 1 tam giác có 3 đỉnh trùng với 3 trong số 18 đỉnh của đa giác đã cho là ![]()
Gọi A là biến cố: “ tam giác được chọn là tam giác cân”.
- TH1: Tam giác được chọn là tam giác đều: có 6 cách.
- TH2: Tam giác được chọn là tam giác cân nhưng không phải tam giác đều:
+ Chọn đỉnh của tam giác cân có 18 cách.
+ Chọn cặp đỉnh còn lại để cùng với đỉnh đã chọn tạo thành đỉnh của tam giác cân (không đều) có 7 cách.
Suy ra số cách chọn tam giác cân nhưng không phải tam giác đều là 18.7 = 126 cách.
Vậy ![]()
![]()
Cho một đa giác đều 24 đỉnh. Hỏi a.Đa giác có bao nhiêu đường chéo. Từ các đỉnh của đa giác lập được bao nhiêu: b,Tam giác vuông c,Tam giác đều d,Tứ giác e,Hình chữ nhật mà không phải là hình vuông
a: Số đường chéo là:
\(\dfrac{24\left(24-3\right)}{2}=12\cdot21=252\)
b: 24 đỉnh =>12 đường kính
chọn 1 đường kính =>Sẽ có 22 điểm còn lại
=>Có 22*12=264 tam giác vuông
Cho một đa giác đều 24 đỉnh. Hỏi a.Đa giác có bao nhiêu đường chéo. Từ các đỉnh của đa giác lập được bao nhiêu: b,Tam giác vuông c,Tam giác đều d,Tứ giác e,Hình chữ nhật mà không phải là hình vuông
a: Số đường chéo là 24*21/2=21*12=336(đường chéo)
b: Số tam giác vuông tạo thành là:12*22=264 tam giác
Cho một đa giác đều 24 đỉnh. Hỏi a.Đa giác có bao nhiêu đường chéo. Từ các đỉnh của đa giác lập được bao nhiêu: b,Tam giác vuông c,Tam giác đều d,Tứ giác e,Hình chữ nhật mà không phải là hình vuông
a. Để tính số đường chéo của một đa giác đều n đỉnh, ta dùng công thức: số đường chéo = n(n-3)/2. Áp dụng vào trường hợp này, ta có số đường chéo của đa giác đều 24 đỉnh là: 24(24-3)/2 = 276 đường chéo.
b. Để lập được một tam giác vuông từ các đỉnh của đa giác đều 24 đỉnh, ta cần chọn 3 đỉnh sao cho 2 trong số đó nằm trên cùng một đường kính của đa giác. Có tổng cộng 24 cách chọn đỉnh trên đường kính và vì mỗi tam giác vuông sẽ được lập bởi 2 đường kính khác nhau, nên số tam giác vuông lập được từ các đỉnh của đa giác đều 24 đỉnh là: 24 x 12 = 288 tam giác vuông. Tuy nhiên, một số tam giác vuông sẽ bị lặp lại khi ta quay đa giác, do đó số tam giác vuông duy nhất là: 288/24 = 12 tam giác vuông.
c. Để lập được một tam giác đều từ các đỉnh của đa giác đều 24 đỉnh, ta cần chọn 3 đỉnh liên tiếp trên đường tròn ngoại tiếp đa giác. Có tổng cộng 24 cách chọn 3 đỉnh liên tiếp, do đó số tam giác đều lập được từ các đỉnh của đa giác đều 24 đỉnh là: 24 tam giác đều.
d. Để lập được một tứ giác từ các đỉnh của đa giác đều 24 đỉnh, ta cần chọn 4 đỉnh bất kỳ. Có tổng cộng C(24,4) cách chọn 4 đỉnh, do đó số tứ giác lập được từ các đỉnh của đa giác đều 24 đỉnh là: C(24,4) = 10626 tứ giác.
e. Để lập được một hình chữ nhật từ các đỉnh của đa giác đều 24 đỉnh, ta cần chọn 4 đỉnh sao cho 2 đỉnh đối diện của hình chữ nhật nằm trên cùng một đường kính của đa giác. Có tổng cộng 24 cách chọn đỉnh trên đường kính và vì mỗi hình chữ nhật sẽ được lập bởi 2 đường kính khác nhau, nên số hình chữ nhật lập được từ các đỉnh của đa giác đều 24 đỉnh là: 24 x 12 = 288 hình chữ nhật. Tuy nhiên, trong số đó có 24 hình vuông, do đó số hình chữ nhật mà không phải là hình vuông là: 288 - 24 = 264 hình chữ nhật.