Cho hình thang ABCD (AB // CD). Một đường thẳng song song với CD, cắt các đoạn thẳng AD, BD, AC, BC theo thứ tự ở M, I, K, N. CMR: MI = KN.
Những câu hỏi liên quan
cho hình thang ABCD (AB // CD) . 1 đường thẳng song song với CD cắt các đoạn thẳng AD,BC,AC,BD.theo thứ tự ở M,I,K,N. chứng minh MI=KN
Cho hình thang ABCD (AB//CD). Một đường thẳng song song với CD cắt các đoạn thẳng AD, BD, AC,BC theo thứ tự ở M, I, K, N. CMR: MI=KNCho hình thang ABCD (AB//CD) có O là giao điểm của AD và BC. Gọi F lag trung điểm của CD. E là giao điểm của OF và AB. CMR: E là trung điểm của AB
Xem chi tiết
SỬ DỤNG CÁC TA- LÉT NHA.
MÌNH ĐANG CẦN GẤP AK. GIẢI BÀI NÀO CŨNG ĐC. CẢM ƠN.
:) à bạn :) nãy mình soạn ra bài đúng r mà nhấn nhầm xoá hết cmnr :))) nên h mình gợi ý thôi nha :(((
bài 1 bạn xét tam giác BCD có NI //CD ( vì MN//CD và I thuộc MN) , =>BN/NC=NI/CD ( hệ quả ...) (1)
xét tam giác ADC r chứng minh tương tự để ra được MK/DC=AM/MD (2)
có AM=BN ( cm ABNM là hbh)
và MD=NC ( cm MNCD là hbh)
=>AM/MD=BN/NC (3)
Từ 1,2,3 => MK/CD=NI/CD
=>MK=CD
=> MI=KN= MK+ KI=NI+KI ( điều phải cm)
Đúng 0
Bình luận (0)
sorry câu gần cuối ghi sai :))) MK=NI nha bạn
Với đề bài 2 sai thì phải :v bởi nếu trong hình thang ABCD có AB//CD thì AD//BC chứ vậy sao O là giao điểm của hai đường thẳng song song được
Đúng 0
Bình luận (0)
cho hình thang abcd ab song song với cd. Một đường thẳng d song song với hai đáy cắt hau cạnh bên ad và bc thứ tự tại m và n và cắt hai đường chéo bd và ac thứ tự tại h, k. CMR: a,MH=KN.
b, hãy nêu cách dựng đoạn thẳng d sao cho MH=HK=KN
Xem chi tiết
a) Xét hình thang ABCD(AB//CD) có
M∈AD(Gt)
N∈BC(gt)
MN//AB//DC(gt)
Do đó: \(\dfrac{AM}{AD}=\dfrac{BN}{BC}\)(Định lí Ta lét)(1)
Xét ΔADC có
M∈AD(Gt)
K∈AC(Gt)
MK//DC(gt)
Do đó: \(\dfrac{AM}{AD}=\dfrac{MK}{DC}\)(Hệ quả của Định lí Ta lét)(2)
Xét ΔBDC có
H∈BD(Gt)
N∈BC(Gt)
HN//DC(gt)
Do đó: \(\dfrac{BN}{BC}=\dfrac{HN}{DC}\)(Hệ quả của Định lí Ta lét)(3)
Từ (1), (2) và (3) suy ra \(\dfrac{MK}{DC}=\dfrac{HN}{DC}\)
⇔MK=HN
⇔MK+KH=HN+KH
⇔MH=NK(đpcm)
Đúng 0
Bình luận (0)
Cầu 4. (2 điểm). Cho hình thang ABCD (AB // CD) . Từ trung điểm M của cạnh bên AD, vẽ một đường thẳng song song với hai đáy lần lượt cắt BD tại I: AC tại K: BC tại N. Tính độ dài các đoạn thẳng MI. KN. IK biet AB=8cm : CD = 12 cm
Cho hình thang ABCD(AB//CD). Một đường thẳng d song song với hai cạnh đáy cắt hai cạnh bên AD,BA theo thứ tự M,N và cắt hai đường chéo BD,AC theo thứ tự ở H,K.
a) CMR MH=KN
b) Hãy nêu cách dựng đường thăng d sao cho MH=HK=KN
cho hình thang ABCD ( AB// CD , AB<CD ) AC cắt BD tại I . Từ I vẽ đường thẳng song song với AB cắt AD và BC theo thứ tự ở M ,N . Chứng minh IM =IN
cho hình thang ABCD ( AB// CD , AB<CD ) AC cắt BD tại I . Từ I vẽ đường thẳng song song với AB cắt AD và BC theo thứ tự ở M ,N . Chứng minh IM =IN
Cho hình thang ABCD(AB//CD).Một đường thẳng d song song với hai cạnh đáy cắt hai cạnh bên Ad,BC theo thứ tự ở M,N và cắt hai đường chéo BD,AC theo thứ tự ở H,K.
a)CMR:MH=KN.
b)Hãy nêu cách dựng đường thẳng d sao cho MH=HK=KN.
Cho hình thang ABCD (AB //CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q chứng minh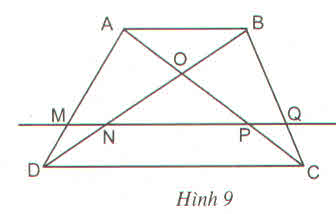 
DN\BD=CP\AC
\(\dfrac{DN}{BD}=\dfrac{CQ}{BC}=\dfrac{CP}{AC}\)
Đúng 0
Bình luận (0)