Bài 1:
a) Tìm tổng của tất cả các số nguyên x thỏa mãn: x2 <2016
b) Có bao nhiêu số nguyên x thỏa mãn(x2 -100)(1-\(|x|\))>0
a, Tìm tất cả các số nguyên x thỏa mãn -11<x<9. Tính tổng tất cả các số nguyên vừa tìm đc
b,Tìm tất cả các số nguyên x thỏa mãn -9<x<10.Tính tổng các số nguyên vừa tìm đc
c,Tìm tất cả các số nguyên x thỏa mãn -15<x<16.Tính tổng tất cả các số nguyên vừa tìm đc
Phần b và c là dấu lớn hơn hoặc bằng nhé !!
MN GIÚP MÌNH VỚI Ạ !!!!
a)
Các số nguyên x thỏa mãn là:
\(x\in\left\{-10;-9;-8;-7;-6;-5;-4;-3;-2;-1;0;1;2;3;4;5;6;7;8\right\}\)
Tổng các số nguyên trên là:
\((8-10).19:2=-19\)
b)
Các số nguyên x thỏa mãn là:
\(x\in\left\{-9;-8;-7;-6;-5;-4;-3;-2;-1;...;6;7;8;9;10\right\}\)
Tổng các số trên là:
\((10-9).20:2=10\)
c) Các số nguyên x thỏa mãn là:
\(x\in\left\{-15;-14;-13;-12;-11;-10;-9;-8;-7;-6;-5;...;12;13;14;15;16\right\}\)
Tổng các số nguyên đó là:
\((16-15).32:2=16\)
tìm tất cả các cặp số nguyên (x, y) thỏa mãn: x(x2 - y) + (y - 3)(x2 + 1) = 0
Tìm tất cả các số nguyên x,y . thỏa mãn phương trình : x2+6xy+5y2-4y-8=0
\(x^2+6xy+5y^2-4y-8=0\)
\(\Leftrightarrow (x^2+6xy+9y^2)-(4y^2+4y+1)=7\)
\(\Leftrightarrow (x+3y)^2-(2y+1)^2=7\)
\(\Leftrightarrow (x+y-1)(x+5y+1)=7\)
Vì x,y nguyên nên ta có các trường hợp sau:
TH1: \(\begin{cases} x+y-1=1\\ x+5y+1=7 \end{cases} \Leftrightarrow \begin{cases} x+y-1=1\\ 4y+2=6 \end{cases} \Leftrightarrow \begin{cases} x=1\\ y=1 \end{cases}\)
Các TH còn lại bạn tự làm nhé
\(x^2+6xy+5y^2-4y-8=0\)
\(\Leftrightarrow\left(x^2+6xy+9y^2\right)-4y^2-4y-1-7=0\)
\(\Leftrightarrow\left(x+3y\right)^2-\left(2y+1\right)^2=7\)
\(\Leftrightarrow\left(x+5y+1\right)\left(x+y-1\right)=7=\left[{}\begin{matrix}1.7\\7.1\\\left(-1\right).\left(-7\right)\\\left(-7\right).\left(-1\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5y+1=1;x+y-1=7\\x+5y+1=7;x+y-1=1\\x+5y+1=-1;x+y-1=-7\\x+5y+1=-7;x+y-1=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=10;y=-2\left(nhận\right)\\x=y=1\left(nhận\right)\\x=y=1\left(nhận\right)\\x=10;y=-2\left(nhận\right)\end{matrix}\right.\)
-Vậy các cặp số (x,y) là \(\left(10;-2\right);\left(1;1\right)\)
tìm tất cả các cặp số nguyên x, y thỏa mãn x2+x = 32019y+1
- Với \(y=0\Rightarrow x^2+x=3^0+1=2\)
\(\Rightarrow x^2+x-2=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
- Với \(y< 0\Rightarrow3^{2019y}\) không phải số nguyên \(\Rightarrow3^{2019y}+1\) không phải số nguyên (loại)
- Với \(y>0\Rightarrow3^{2019y}⋮3\Rightarrow3^{2019y}+1\) chia 3 dư 1
Mà \(x^2+x=x\left(x+1\right)\) là tích 2 số nguyên liên tiếp nên chia 3 chỉ có thể dư 0 hoặc 2
\(\Rightarrow x^2+x\ne3^{2019y}+1\) với mọi \(y>0\) \(\Rightarrow\) phương trình ko có nghiệm nguyên
Vậy pt đã cho có đúng 2 cặp nghiệm nguyên là \(\left(x;y\right)=\left(-2;0\right);\left(1;0\right)\)
@ Ha Dung vì khi y < 0 thì y = -k (k N)
⇒ 32019y = 3-2019k = ( N)
()2019k không phải là số nguyên vậy 32019y không phải là số nguyên em nhé.
Tìm tất cả các số nguyên x, y thỏa mãn x2+y2+xy-x-y=1
tìm tổng tất cả các số nguyên x thỏa mãn:
- 5 < x < 0
Vì \(-5\)< \(x\)<\(0\)
\(x\in Z\)
\(\Rightarrow\)\(x\in\text{ }\left\{-4;-3;-2;-1\right\}\)
\(\Rightarrow\)Tổng tất cả các số nguyên x thỏa mãn:
\(\left(-4\right)+\left(-3\right)+\left(-2\right)+\left(-1\right)\)\(=\)\(-10\)
Trả lời:
Vì \(-5< x< 0\)
Mà\(x\inℤ\)
\(\Rightarrow x\in\left\{-4;-3;-2;-1;\right\}\)
Vậy tổng tất cả các số nguyên x thỏa mãn là:
\((-4)+(-3)+(-2)+(-1)=-10\)
Vậy tổng tất cả các số nguyên x thỏa mãn -5 < x < 0 bằng -10.
Hok tốt!
Vuong Dong Yet
Biết rằng trong tất cả các cặp (x; y) thỏa mãn: log 2 x 2 + y 2 + 2 ≤ log 2 x + y - 1 . Chỉ có duy nhất một cặp (x; y) thỏa mãn: 3x + 4y - m = 0 . Khi đó hãy tính tổng tất cả các giá trị m tìm được?
A. 20
B. 46
C. 28
D. 14
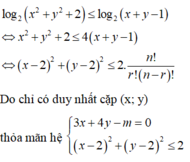
nên đường thẳng 3x + 4y - m = 0 là tiếp tuyến của đường tròn (x – 2)2 + (y – 2)2 = 2.
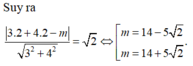
Chọn C.
a) Tìm tất cả các số nguyên x thỏa mãn :-10< x < 15
b) Tính tổng tất cả các số nguyên vừa tìm được.
a) x\(\in\)\(\left\{-9;-8;-7;-6;;...;0;....;14\right\}\)
b)\(-9+\left(-8\right)+\left(-7\right)+\left(-6\right)+...+0+....+13+14\)\(=\left[-9+9\right]+\left[-8+8\right]+\left[-7+7\right]+\left[-6+6\right]+...+0+10+11+...+14\)
=\(0+10+11+12+13+14\)
=\(60\)
a) x thuộc {-9;-8;-7;...;14}
b) [-9+9]+[-8+8]+[-7+7]+...+10+11+12+13+14
= 0+10+11+12+13+14
=60
Tìm tổng tất cả các số nguyên x thỏa mãn
a) tổng tất cả các số nguyên x có giá trị tuyệt đối nhỏ hơn hoặc bằng 15
Vì giá trị tuyệt đối của x < 15
Mà x thuộc z
Nên x thuộc { -15; -14;-13;............13;14;15 }
Tổng các số nguyên x có giá trị tuyệt đối x < 15
(-15)+(-14)+(-13)+............+13+14+15
=[(-15)+15] + [(-14)+14] +[(-13)+13]+......+[(-1)+1]+0
= 0+0+0+.........+0+0
=0
Vậy tổng số nguyên x thỏa mản điều kiện giá trị tuyệt đối của x < 15 là 0