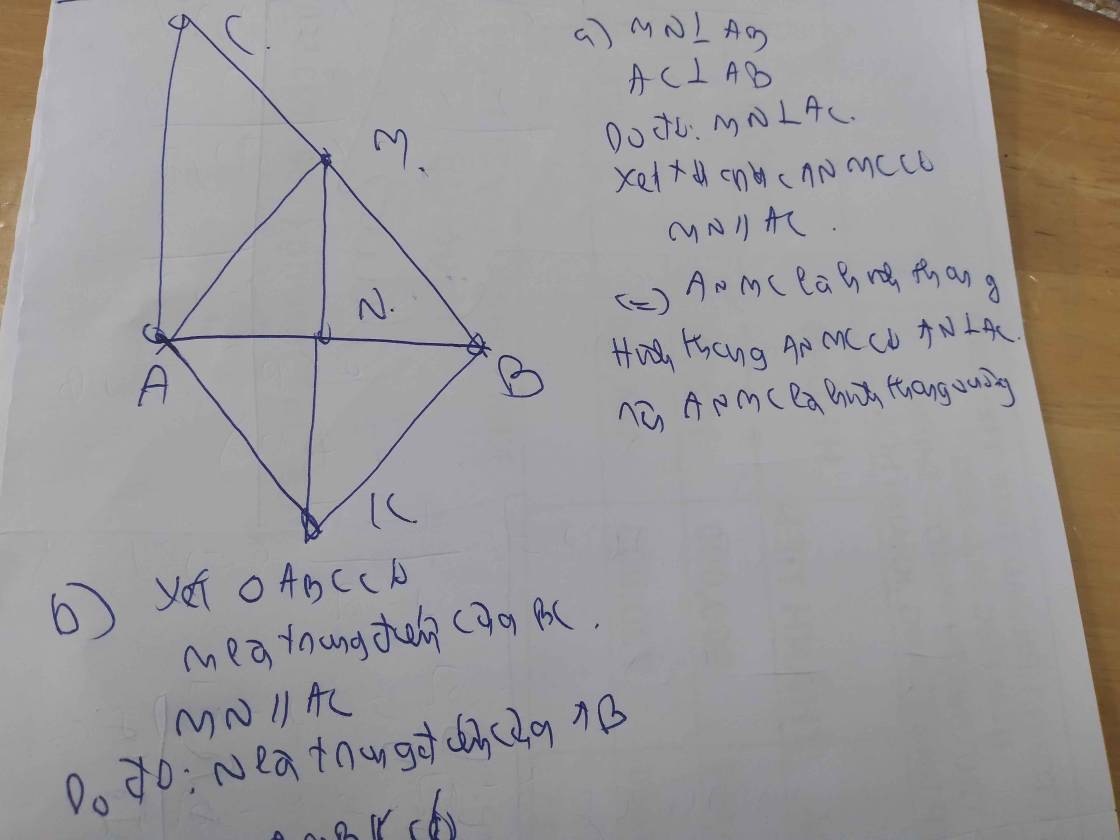
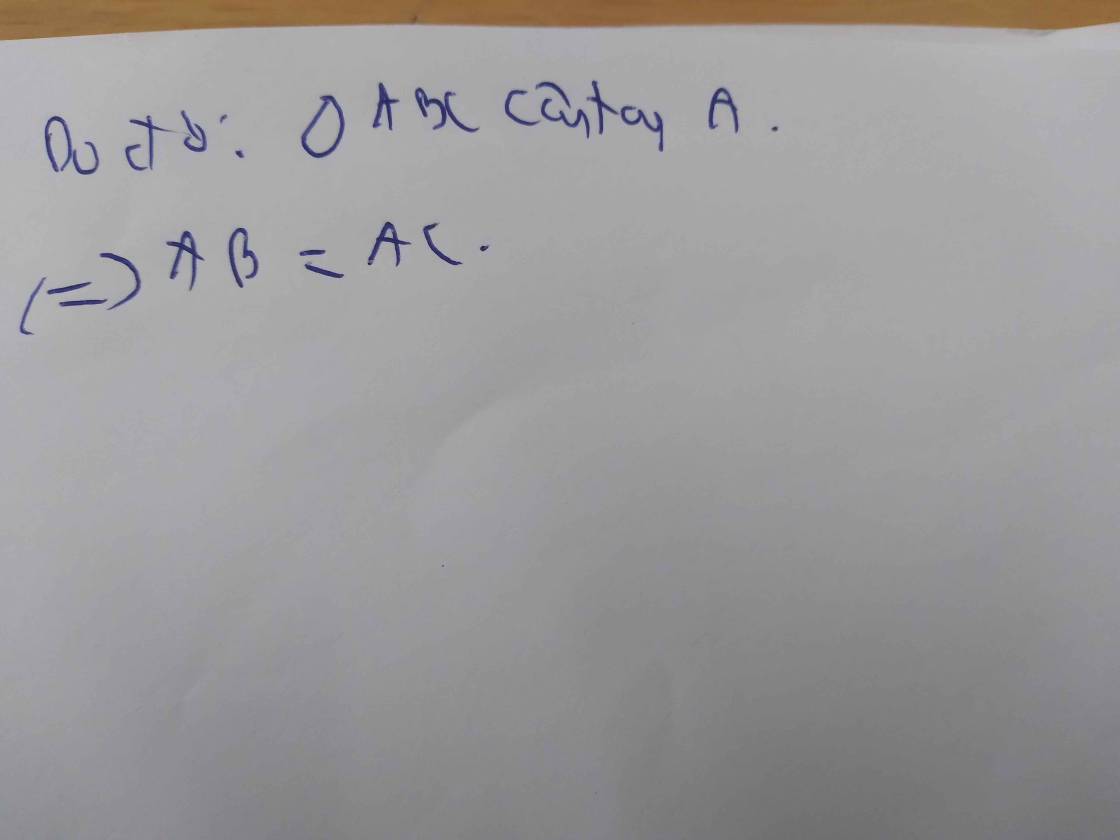Cho tam giác ABC có M, N di chuyển trên AB, AC( M,N khác A,B,C). của tam giác thoả mãn điều kiện AM.AN=BM.CN. Tìm tập hợp trung điểm K của MN

Những câu hỏi liên quan
Cho tam giác ABC cân tại A. cho M, N di chuyển trên AB, AC và AM=CN. TÌM tập hợp các trung điểm I của MN
không viết lại đề nha =))).Nhớ tích đúng cho mình nha =)) <3
x^2 - 4 + x^2 -4x + 4 = 2x(x-2)
(x^2 +x^2) + (-4 +4)- 4x = 2x^2-4x
2x^2 - 0-4x =2x^2 - 4x
2x^2 - 4x = 2x^2- 4x
Đây nha =))))
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi I là trung điểm của cạnh BC. Đường phân giác của góc AIB cắt cạnh AB ở M. Đường phân giác của góc AIC cắt cạnh AC ở N.
a) Chứng minh rằng MM // BC.
b) Tam giác ABC phải thoả điều kiện gì để có MN = AI?
c) Tam giác ABC phải thoả điều kiện gì để có MN vuông góc AI
Cho tam giác ABC. Gọi I là trung điểm của cạnh BC. Đường phân giác của góc AIB cắt cạnh AB ở M. Đường phân giác của góc AIC cắt cạnh AC ở N. a) Chứng minh rằng MM // BC. b) Tam giác ABC phải thoả điều kiện gì để có MN = AI? c) Tam giác ABC phải thoả điều kiện gì để có MN vuông góc AI?
mn làm giúp m với ( ko cần vẽ hình nhé ) đg cần gấp.
a) Kẻ MN
Có: IM là tia p/g của góc AIB
=> AM:BM = AI:BI (1)
IN là tia p/g của góc AIC
=> AN:NC = AI:IC (2)
Từ (1) và (2) => BI =CI
=> AM:MB = AN:NC
=> MN // BC ( Talet đảo )
mik cũng ko làm đc
Cho tam giác ABC. Gọi I là trung điểm của cạnh BC. Đường phân giác của góc AIB cắt cạnh AB ở M. Đường phân giác của góc AIC cắt cạnh AC ở N.
a) Chứng minh rằng MN // BC.
b) Gọi K là giao điểm của MN và AI. Chứng minh K là trung điểm MN.
c) Tam giác ABC phải thoả mãn điều kiện gì để có MN vuông góc với AI?
Bạn dưới làm câu a) rồi mình xin phép làm từ câu b) nhé :
b) Áp dụng định lý Talets ta có :
+) \(MK//BI\Rightarrow\frac{KM}{BI}=\frac{AK}{AI}\)
+) \(KN//IC\Rightarrow\frac{AK}{AI}=\frac{KN}{IC}\)
\(\Rightarrow\frac{KM}{BI}=\frac{KN}{IC}\) mà \(BI=CI\)
\(\Rightarrow KM=KN\)
Nên K là trung điểm của MN.
c) Ta thấy : \(MN//BC\)
Vì thế, để \(MN\perp AI\)
\(\Leftrightarrow AI\perp BC\)
\(\Leftrightarrow\Delta ABC\) cân tại A ( Do \(AI\) vừa là trung tuyến, vừa là đường cao )
\(\Leftrightarrow AB=AC\)
Vậy \(\Delta ABC\) có thêm điều kiện \(AB=AC\) thì \(MN\perp AI\)
a) Kẻ đoạn thẳng MN
Ta có: IM là tia phân giác \(\widehat{AIB}\)
\(\Rightarrow\frac{AM}{BM}=\frac{AI}{BI}\left(1\right)\)
IN là tia phân giác \(\widehat{AIC}\)
\(\Rightarrow\frac{AN}{NC}=\frac{AI}{IC}\left(2\right)\)
Từ (1) (2) và BI = CI
\(\Rightarrow\frac{AM}{MB}=\frac{AN}{NC}\)
=> MN // BC (định lý Ta lét đảo)
Hình bạn tự vẽ nha, thanks bạn ![]()
a) Xét ΔABCΔABC, có:
M,N lần lượt là trung điểm của AB,AC
⇒⇒MN là đường trung bình của ΔABCΔABC
⇒⇒MN//BC
⇒⇒BMNC là hình thang
b) AMKN không phải AMNK nha bạn
Xét ΔABKΔABK, có:
M là trung điểm của AB
MI//BK(I∈∈MN ; K∈BCK∈BC mà MN//BC)
⇒⇒MI là đường trung bình của ΔABKΔABK
⇒⇒I là trung điểm của AK
Lại có: I là trung điểm của MN(gt)
Do đó: AMKN là hình bình hành (dhnb số 4)
c)Tam giác ABC là tam giác cân tại A thì:
AM=12ABAM=12AB
AN=12ACAN=12AC
Mà AB=AC(ΔABCΔABC cân tại A)
⇒AM=AN⇒AM=AN
Mà AMKN là hình bình hành
⇒⇒AMKN là hình thoi
d)Bài này hơi bị khó luôn ấy
Ta có: MK//AN(AMKN là hình bình hành)
⇒⇒MK//AH(H∈∈AN)
Mà KH⊥⊥AH(H∈∈AC mà KH⊥⊥AC)
⇒⇒KH⊥⊥MK
⇒MKHˆ=90o⇒MKH^=90o
Xét ΔAKBΔAKB vuông tại K, có:
KM là đường trung tuyến
⇒AM=KM=BM⇒AM=KM=BM
⇒ΔBMK⇒ΔBMK cân tại M
⇒Bˆ=MKBˆ⇒B^=MKB^
Ta cũng có: AMEˆ=BˆAME^=B^(đồng vị; E∈∈MN mà MN//BC nên ME//BC)
Mà KMEˆ=MKBˆKME^=MKB^(so le trong và ME//BC)
Do đó: AMEˆ=KMEˆAME^=KME^
Xét ΔAMEΔAME và ΔKMEΔKME, có:
AM=KM(cmt)
AMEˆ=KMEˆ(cmt)AME^=KME^(cmt)
ME: chung
Do đó: ΔAME=ΔKMEΔAME=ΔKME
⇒MAEˆ=MKEˆ=90o⇒MAE^=MKE^=90o
⇒ΔAME⇒ΔAME là tam giác vuông tại A
Xem thêm câu trả lời
cho ta giác ABC cân tại B , đường trung tuyến BN. gọi K là trung điểm BC, H là điểm đối xứng với N qua điểm K
a) tứ giác BNCH là hình gì ? vì sao
b) tứ giác ABHN là hình gì ? vì sao?
c) tìm điều kiện của tam giác ABC, điểm M di chuyển trên cạnh AC. kẻ ME song song BC ,MF song song AB( E thuộc AB F thuộc BC ). trung điểm O của EF chuyển động trên đường gì.
câu c dư nha tìm điều kiện của tam giác ABC để tứ giác BNCH là hình vuông
nha giúp với
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, M là trung điểm của BC.Kẻ MN vuông góc với AB tại N(N thuộc AB) a)CM:tứ giác ANMC là Hình Thang Vuông b) Trên Tia MN lấy K sao cho N là trung Điểm MK. CM tứ giác AKBM là hình thoi c)Tam Giác ABC cần Thêm Điều Kiện Gì Để tứ giác AKBM là hình vuông
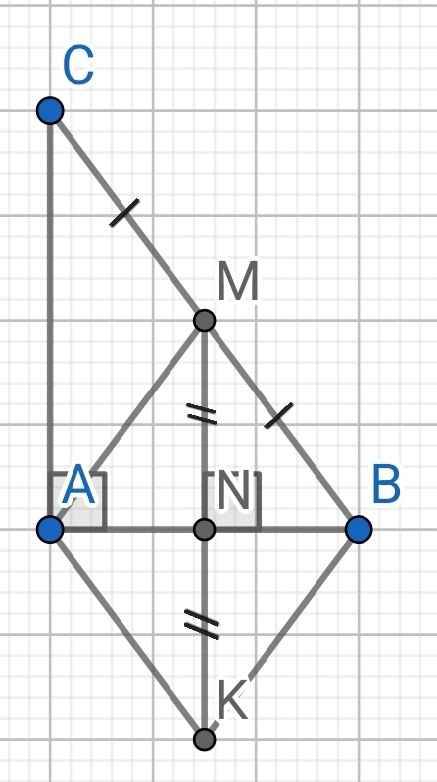 a) Do MN ⊥ AB (gt)
a) Do MN ⊥ AB (gt)
AC AB (do ∆ABC vuông tại A)
⇒ MN // AC
Tứ giác ANMC có:
MN // AC (cmt)
⇒ ANMC là hình thang
Mà ∠CAN = 90⁰
⇒ ANMC là hình thang vuông
b) ∆ABC có:
MN // AC (cmt)
M là trung điểm của BC
⇒ N là trung điểm của AB
Do MN ⊥ AB (gt)
⇒ MK ⊥ AB
Tứ giác AKBM có:
N là trung điểm của AB (cmt)
N là trung điểm của MK (gt)
⇒ AKBM là hình bình hành
Mà MK ⊥ AB (cmt)
⇒ AKBM là hình thoi
c) Để AKBM là hình vuông thì
AM ⊥ MB
⇒ AM ⊥ BC
⇒ AM là đường cao của ∆ABC
Mà AM là đường trung tuyến của ∆ABC (do M là trung điểm của BC)
⇒ ∆ABC có AM vừa là đường cao, vừa là đường trung tuyến
⇒ ∆ABC cân tại A
Mà ∆ABC vuông tại A (gt)
⇒ ∆ABC vuông cân tại A
Vậy để AKBM là hình vuông thì ∆ABC vuông cân tại A
Đúng 1
Bình luận (0)
1, Cho tam giác ABC , M, N lần lượt là trung điểm của AB , AC a, Tứ giác BMNC là hình gì ? b, Gọi I là trung điểm của MN , đường thẳng AI cắt BC tại K . Tứ giác AMKN là hình gì ? Vì sao ? c, Tam giác ABC cần điều kiện gì để AMKN là hình thoi . d, Vói điều kiện trên của tam giác ABC . Vẽ KH vuông góc với AC tại H . Đường thẳng KH cắt MN tại E . Chứng minh tam giác AME vuông 2, Cho tam giác ABC cân tai A lấy điểm M trên cạnh AB . Từ M kẻ đường thẳng song song với AC cắt BC tại E a, Chứng minh tam...
Đọc tiếp
1, Cho tam giác ABC , M, N lần lượt là trung điểm của AB , AC
a, Tứ giác BMNC là hình gì ?
b, Gọi I là trung điểm của MN , đường thẳng AI cắt BC tại K . Tứ giác AMKN là hình gì ? Vì sao ?
c, Tam giác ABC cần điều kiện gì để AMKN là hình thoi .
d, Vói điều kiện trên của tam giác ABC . Vẽ KH vuông góc với AC tại H . Đường thẳng KH cắt MN tại E . Chứng minh tam giác AME vuông
2, Cho tam giác ABC cân tai A lấy điểm M trên cạnh AB . Từ M kẻ đường thẳng song song với AC cắt BC tại E
a, Chứng minh tam giác BME cân
b, Trên tia đối của tia CA lấy điểm N sao cho CN = BM . Tứ giác MCNE là hình gì ?
c, Gọi I là trung điểm của CE . Chứng minh M,N,I thẳng hàng
d, Từ M kẻ đường thẳng song song với BC cắt AC tại F . Từ N kẻ đường thẳng song song với BC cắt Me tại K . Chứng minh F,I,K thẳng hàng
Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
hay BMNC là hình thang
b: Xét ΔABK có MI//BK
nên MI/BK=AM/AB=1/2(1)
XétΔACK có NI//CK
nên NI/CK=AN/AC=1/2(2)
Từ (1)và (2) suy ra MI/BK=NI/CK
mà MI=NI
nên BK=CK
hay K là trug điểm của BC
Xét ΔABC có
K là trung điểm của BC
M là trung điểm của AB
Do đó: KM là đường trung bình
=>KM//AN và KM=AN
hay AMKN là hình bình hành
Đúng 0
Bình luận (0)
Bài 1c) Cho tam giác ABC cân tại A, phân giác BD. Biết góc BAC120 độ. Tính các cạnh của tam giácBài 2: Cho tam giác ABC cân ở A, BC8cm, phân giác của góc B cắt đường cao AH ở K, AK/AH3/5. a) Tính độ dài AB (câu này tớ làm đc rồi)b) Đường thẳng vuông góc với BK tại B cắt AH ở E. Tính EH (còn mỗi câu này thôi)Bài 3: Cho tam giác ABC cân, có BABCa, ACb. Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại Na) Cm: MN//AC b) Tính MN theo a,bBài 4: Cho tam giác ABC cân ở A, phân giác t...
Đọc tiếp
Bài 1c) Cho tam giác ABC cân tại A, phân giác BD. Biết góc BAC=120 độ. Tính các cạnh của tam giác
Bài 2: Cho tam giác ABC cân ở A, BC=8cm, phân giác của góc B cắt đường cao AH ở K, AK/AH=3/5.
a) Tính độ dài AB (câu này tớ làm đc rồi)
b) Đường thẳng vuông góc với BK tại B cắt AH ở E. Tính EH (còn mỗi câu này thôi)
Bài 3: Cho tam giác ABC cân, có BA=BC=a, AC=b. Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N
a) Cm: MN//AC
b) Tính MN theo a,b
Bài 4: Cho tam giác ABC cân ở A, phân giác trong BD, BC=10cm, AB=15cm
a) Tính AD, DC
b) Đường phân giác ngoài góc B của tam giác ABC cắt đường thẳng AC tại D'. Tính D'C
Bài 5: Cho tam giác ABC có AB=5cm, AC=6cm, BC=7cm. Gọi G là trọng tâm tam giác ABC, O là giao điểm của 2 đường phân giác BD, AE
a) Tính độ dài đoạn thẳng AD
b) Cm: OG//AC
HD: a) AD=2,5cm b) OG//DM => OG//AC
Bài 6: Cho tam giác ABC. Gọi I là trung điểm của cạnh BC. Đường phân giác của góc AIB cắt cạnh AB ở M. Đường phân giác của góc AIC cắt cạnh AC ở N
a) CMR: MN//BC
b) Gọi giao điểm của DE và AM là O. CM: OM=ON
c) Tam giác ABC phải thoả mãn điều kiện gì để có MN=AI
d) Tam giác ABC phải thoả mãn điều kiện gì để có MN vuông góc với AI
Cho tam giác ABC vuông tại A, AB3cm, AC4cm, AM là trung tuyến của tam giác ABCA. Tính BC, AMB. Kẻ MD vuông gíc với AB, ME vuông góc với AC. CM. Tứ giác AEMD là hình chữ nhậtC. CM D là trung điểm của AB, E là trung điểm của ACD. Tứ giác DECB là hình gì? Vì sao?E. Tìm điều kiện của tam giác ABC để AEMD là hình vuôngF. Khi M di chuyển trên cạnh BC thì trung điểm I của AM di chuyển trên đường nào?
Đọc tiếp
Cho tam giác ABC vuông tại A, AB=3cm, AC=4cm, AM là trung tuyến của tam giác ABC
A. Tính BC, AM
B. Kẻ MD vuông gíc với AB, ME vuông góc với AC. CM. Tứ giác AEMD là hình chữ nhật
C. CM D là trung điểm của AB, E là trung điểm của AC
D. Tứ giác DECB là hình gì? Vì sao?
E. Tìm điều kiện của tam giác ABC để AEMD là hình vuông
F. Khi M di chuyển trên cạnh BC thì trung điểm I của AM di chuyển trên đường nào?