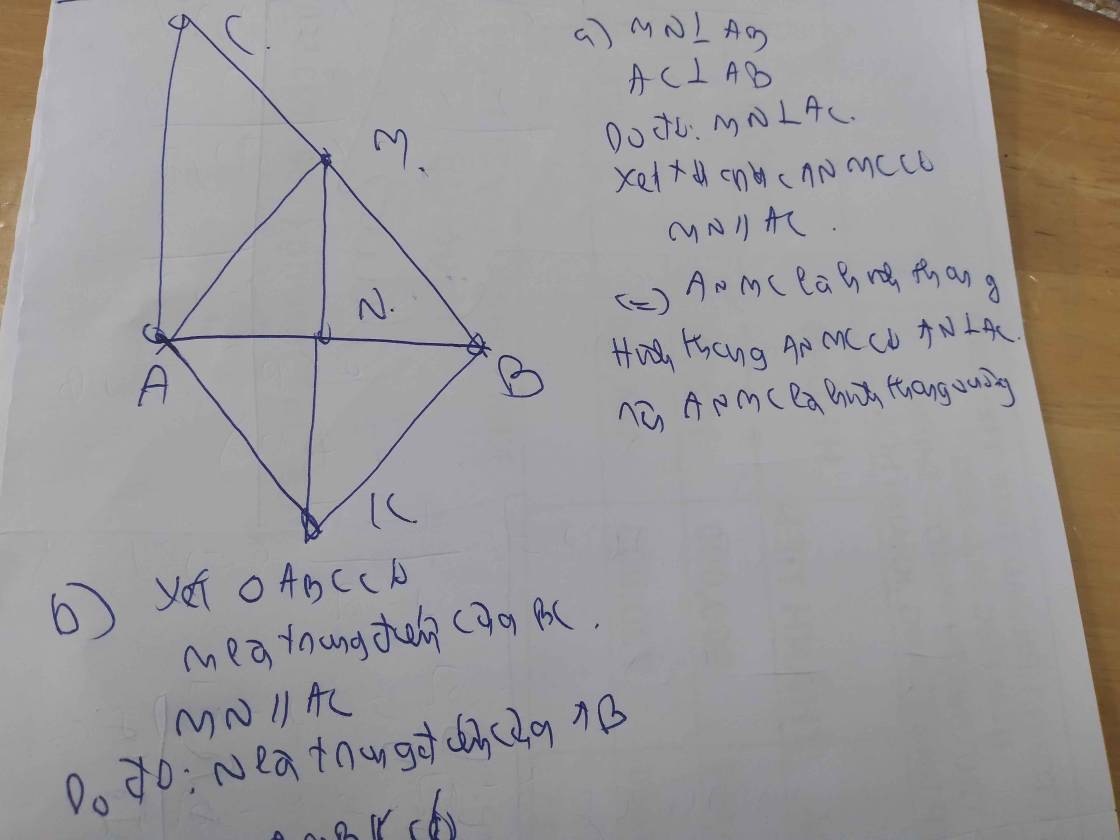
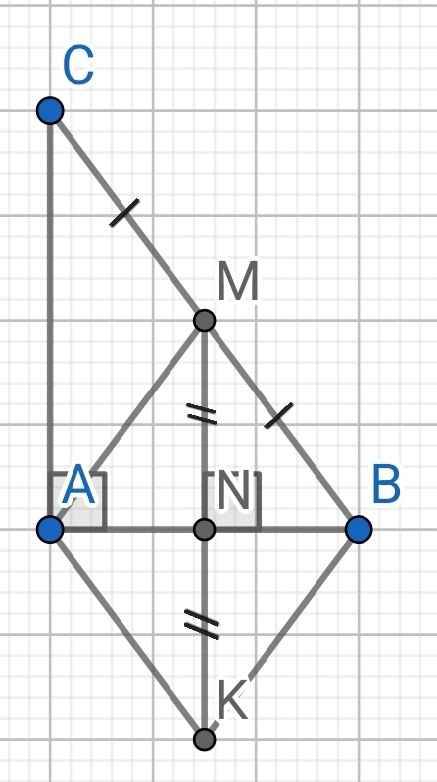
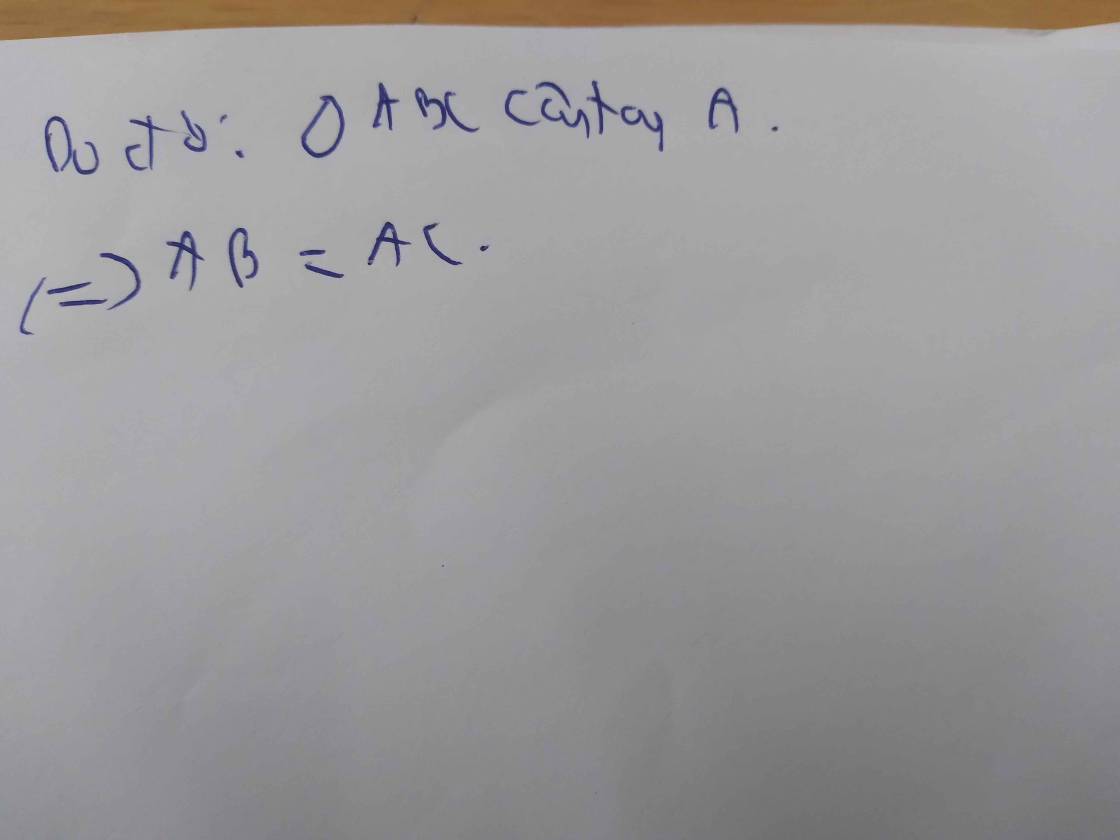 a) Do MN ⊥ AB (gt)
a) Do MN ⊥ AB (gt)
AC AB (do ∆ABC vuông tại A)
⇒ MN // AC
Tứ giác ANMC có:
MN // AC (cmt)
⇒ ANMC là hình thang
Mà ∠CAN = 90⁰
⇒ ANMC là hình thang vuông
b) ∆ABC có:
MN // AC (cmt)
M là trung điểm của BC
⇒ N là trung điểm của AB
Do MN ⊥ AB (gt)
⇒ MK ⊥ AB
Tứ giác AKBM có:
N là trung điểm của AB (cmt)
N là trung điểm của MK (gt)
⇒ AKBM là hình bình hành
Mà MK ⊥ AB (cmt)
⇒ AKBM là hình thoi
c) Để AKBM là hình vuông thì
AM ⊥ MB
⇒ AM ⊥ BC
⇒ AM là đường cao của ∆ABC
Mà AM là đường trung tuyến của ∆ABC (do M là trung điểm của BC)
⇒ ∆ABC có AM vừa là đường cao, vừa là đường trung tuyến
⇒ ∆ABC cân tại A
Mà ∆ABC vuông tại A (gt)
⇒ ∆ABC vuông cân tại A
Vậy để AKBM là hình vuông thì ∆ABC vuông cân tại A