| Câu 11: Trong mặt phẳng Oxy , cho ba vectơ a b c = = - = - (1;2), ( 3;1), ( 4;2) | . Chọn |
. Biết u a b c = + + 3 2 4 khẳng định đúng.
A. u
cùng phương với i
. B. u
không cùng phương với i
.
C. u
cùng phương với j
| . |
D. u
vuông góc với i
Trong mặt phẳng Oxy cho ba vectơ a→ = (0;1) ; b→ = (-1;2) ; c→ = (-3;-2) tọa độ của vectơ U→ = 3a→ +2b→ -4c→ là...
Trong mặt phẳng tọa độ Oxy, cho hai vectơ a → = − 3 ; 2 và b → = − 1 ; − 7 . Tìm tọa độ vectơ c → biết c → . a → = 9 và c → . b → = − 20.
A. c → = − 1 ; − 3 .
B. c → = − 1 ; 3 .
C. c → = 1 ; − 3 .
D. c → = 1 ; 3 .
Gọi c → = x ; y .
Ta có c → . a → = 9 c → . b → = − 20 ⇔ − 3 x + 2 y = 9 − x − 7 y = − 20 ⇔ x = − 1 y = 3 ⇒ c → = − 1 ; 3 .
Chọn B
Trong mặt phẳng tọa độ Oxy, cho hai vectơ a → = − 3 ; 2 và b → = − 1 ; − 7 . Tìm tọa độ vectơ c → biết c → . a → = 9 và c → . b → = − 20.
A. c → = − 1 ; − 3 .
B. c → = − 1 ; 3 .
C. c → = 1 ; − 3 .
D. c → = 1 ; 3 .
Gọi c → = x ; y .
Ta có c → . a → = 9 c → . b → = − 20 ⇔ − 3 x + 2 y = 9 − x − 7 y = − 20 ⇔ x = − 1 y = 3 ⇒ c → = − 1 ; 3 .
Chọn B.
CÁC BÁC ƠI ! GIÚP EM VỚI ☘
Trong mặt phẳng Oxy cho 2 điểm A(4;1) và B(0;-2)
a, Tính tọa độ của vectơ \(\overrightarrow{BA}\)
b, Tìm tọa độ điểm C sao cho \(\Delta\)ABC \(\perp\)C
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có trọng tâm G ( minh họa ở Hình 20)
a) Biểu diễn vectơ \(\overrightarrow {OG} \) theo ba vectơ \(\overrightarrow {OA} \) , \(\overrightarrow {OB} \)và \(\overrightarrow {OC} \)
b) Tìm tọa độ G theo tọa độ của A, B, C
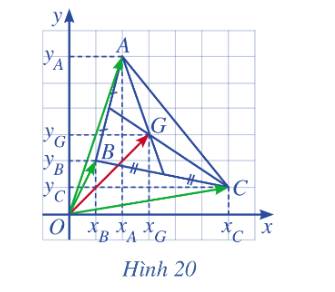
a) Ta có vectơ \(\overrightarrow {OG} \) theo ba vectơ \(\overrightarrow {OA} \) , \(\overrightarrow {OB} \)và \(\overrightarrow {OC} \) là: \(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\)
b) Do tọa độ ba điểm A , B và C là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right),C\left( {{x_C},{y_C}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right),\overrightarrow {OC} = \left( {{x_C},{y_C}} \right)\)
Vậy\(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = \frac{1}{3}\left( {{x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C}} \right) = \left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)
Tọa độ điểm G chính là tọa độ của vectơ \(\overrightarrow {OG} \) nên tọa độ G là \(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)
Trong mặt phẳng tọa độ Oxy, cho A (2; 1), B (-2; 5) và C (-5; 2).
a) Tìm tọa độ của các vectơ \(\overrightarrow {BA} \) và \(\overrightarrow {BC} \)
b) Chứng minh rằng A, B, C là ba đỉnh của một tam giác vuông. Tính diện tích và chu vi của tam giác đó.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
d) Tìm tọa độ của điểm D sao cho tứ giác BCAD là một hình bình hành.
a) Ta có: \(\overrightarrow {BA} = (2 - ( - 2);1 - 5) = (4; - 4)\) và \(\overrightarrow {BC} = ( - 5 - ( - 2);2 - 5) = ( - 3; - 3)\)
b)
Ta có: \(\overrightarrow {BA} .\overrightarrow {BC} = 4.( - 3) + ( - 4).( - 3) = 0\)
\( \Rightarrow \overrightarrow {BA} \bot \overrightarrow {BC} \) hay \(\widehat {ABC} = {90^o}\)
Vậy tam giác ABC vuông tại B.
Lại có: \(AB = \left| {\overrightarrow {BA} } \right| = \sqrt {{4^2} + {{( - 4)}^2}} = 4\sqrt 2 \); \(BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{3^2} + {{( - 3)}^2}} = 3\sqrt 2 \)
Và \(AC = \sqrt {A{B^2} + B{C^2}} = 5\sqrt 2 \) (do \(\Delta ABC\)vuông tại B).
Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}.AB.BC = \frac{1}{2}.4\sqrt 2 .3\sqrt 2 = 12\)
Chu vi tam giác ABC là: \(AB + BC + AC = 4\sqrt 2 + 3\sqrt 2 + 5\sqrt 2 = 12\sqrt 2 \)
c) Tọa độ của trọng tâm G là \(\left( {\frac{{2 + ( - 2) + ( - 5)}}{3};\frac{{1 + 5 + 2}}{3}} \right) = \left( {\frac{{ - 5}}{3};\frac{8}{3}} \right)\)
d) Giả sử điểm D thỏa mãn BCAD là một hình bình hành có tọa độ là (a; b).

Ta có: \(\overrightarrow {CB} = ( 3; 3)\) và \(\overrightarrow {AD} = (a - 2;b - 1)\)
Vì BCAD là một hình bình hành nên \(\overrightarrow {AD} = \overrightarrow {CB} \)
\(\begin{array}{l} \Leftrightarrow (a - 2;b - 1) = ( 3;3)\\ \Leftrightarrow \left\{ \begin{array}{l}a - 2 = 3\\b - 1 = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 5 \\b = 4\end{array} \right.\end{array}\)
Vậy D có tọa độ (5; 4)
Trong mặt phẳng Oxy cho vectơ a→(-3; 1) và b→(2; 2). Hãy tính tích vô hướng a→.b→.
Trong mặt phẳng tọa độ Oxy, cho hai vectơ a → = 4 ; 3 và b → = 1 ; 7 . Tính góc giữa hai vectơ a → và b →
A.900
B. 600
C. 450
D. 300
Ta có cos a → , b → = a → . b → a → . b → = 4.1 + 3.7 16 + 9 . 1 + 49 = 2 2 ⇒ a → , b → = 45 0 .
Chọn C.
4. Trong mặt phẳng toạ độ Oxy cho đg thẳng d có pt 2x -y +1=0. Để phép tịnh tiến theo vectơ v biến d thành chính nó thì vectơ v phải là vectơ nào ? Tại sao?
A. Vectơ v = (2;1)
B. Vectơ v = (2;-1)
C. Vectơ v= (1;2)
D. Vectơ v (-1;2)
15. Trong mặt phẳng với hệ trục toạ độ Oxy , cho các điểm A(-2;1) và B(2;-3). Phép tịnh tiến theo vectơ v biến điểm B thành điểm A . Hãy tìm toạ độ của vectơ u.
4.
Bạn nhớ tính chất sau: phép tịnh tiến theo vecto $\overrightarrow{v}$ biến đường thẳng thành chính nó khi và chỉ khi $\overrightarrow{v}$ là vecto chỉ phương của đường thẳng $d$.
Dễ thấy $\overrightarrow{u_d}=(1,2)$ nên $\overrightarrow{v}=(1,2)$. Đáp án C.
Giải theo cách thuần thông thường:
Gọi vecto cần tìm là $\overrightarrow{v}=(a,b)$
Gọi $M(x,2x+1)$ là điểm thuộc đường thẳng $d$
$M'(x',y')=T_{\overrightarrow{v}}(M)\in (d)$
\(\Rightarrow \left\{\begin{matrix} x'=x+a; y'=2x+1+b\\ 2x'-y'+1=0\end{matrix}\right.\)
\(\Rightarrow 2(x+a)-(2x+1+b)+1=0\)
\(\Leftrightarrow 2a=b\)
Vậy $\overrightarrow{v}=(1,2)$
15.
Gọi $\overrightarrow{v}=(a,b)$
Theo bài ra ta có:
$T_{\overrightarrow{v}}(B)=A$
$\Leftrightarrow \overrightarrow{BA}=\overrightarrow{v}$
$\Leftrightarrow (-4,4)=\overrightarrow{v}$