Xét sự biến thiên và vẽ đồ thị của các hàm số sau:
a) y=x2-2x
c) y=2x2+6x+3
Những câu hỏi liên quan
Xét sự biến thiên và vẽ đồ thị của các hàm số sau:
a) y=x2-2x
c) y=2x2+6x+3
Cho P: y=ax2+bx+1. Tìm a,b để:
(P) đi qua B(-1;6) và có tung độ đỉnh là -3.
Bài 2:
Ta có: \(\dfrac{-\text{Δ}}{4a}=-3\)
\(\Leftrightarrow-\text{Δ}=-12a\)
\(\Leftrightarrow b^2-4a=12a\)
\(\Leftrightarrow b^2-16a=0\left(1\right)\)
Thay x=-1 và y=6 vào (P), ta được:
\(a\cdot\left(-1\right)^2+b\left(-1\right)+1=6\)
\(\Leftrightarrow a-b=5\)
\(\Leftrightarrow a=b+5\)(2)
Thay (2) vào (1), ta được:
\(b^2-16\left(b+5\right)=0\)
\(\Leftrightarrow b^2-16b+64-144=0\)
\(\Leftrightarrow\left(b-8\right)^2=144\)
\(\Leftrightarrow\left[{}\begin{matrix}b=20\\b=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=25\\a=1\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:a. yx3-3x+2b. yx3+1c. y -x3+3x+1d. y-x3-5x2-9x-4e. yx4-2x2-1f. y -dfrac{x^4}{2}-x2+dfrac{3}{2}g. y2x2-x4
Đọc tiếp
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a. y=x3-3x+2
b. y=x3+1
c. y= -x3+3x+1
d. y=-x3-5x2-9x-4
e. y=x4-2x2-1
f. y= \(-\dfrac{x^4}{2}\)-x2+\(\dfrac{3}{2}\)
g. y=2x2-x4
Mọi người giúp mình câu c với ạ, làm mãi đáp án nó vẫn sai qatrou T-T
Bài 2: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a/ y = x2 + 6x + 5
b/ y = x2 - 4x
c/ y = -x2 - 2
d/ y = -x2 + 4x - 4
Xét chiều biến thiên và vẽ đồ thị của các hàm số: y = √x2
Hàm s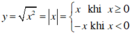ố 
có :
+ Tập xác định D = R.
+ Trên (–∞; 0), hàm số y = –x nghịch biến.
Trên (0 ; +∞), hàm số y = x đồng biến.
Bảng biến thiên :
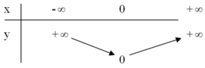
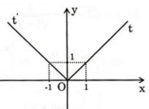
+ Đồ thị hàm số gồm hai phần:
Phần thứ nhất: Nửa đường thẳng y = –x giữ lại phần bên trái trục tung.
Phần thứ hai: Nửa đường thẳng y = x giữ lại phần bên phải trục tung.
Đúng 0
Bình luận (0)
Cho hàm số : y = x 3 – 3 x 2 . Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.
TXĐ: D = R
Sự biến thiên:
y′ = 3 x 2 – 6x = 3x(x – 2)
y′=0 ⇔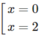 
Hàm số đồng biến trên mỗi khoảng (– ∞ ;0), (2;+ ∞ )
Hàm số nghịch biến trên khoảng (0; 2).
Hàm số đạt cực đại tại x = 0 ; y CĐ = y(0) = 0
Hàm số đạt cực tiểu tại x = 2; y CT = y(2) = -4.
Giới hạn: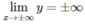 
Điểm uốn: y” = 6x – 6, y” = 0 ⇔ x = 1; y(1) = –2
Suy ra đồ thị có điểm uốn I(1; -2)
Bảng biến thiên:
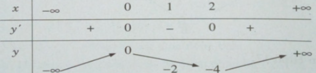
Đồ thị:
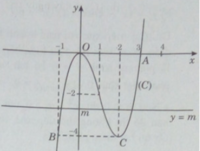
Đồ thị cắt trục hoành tại O(0;0), A(3;0). Đồ thị đi qua điểm B(-1;-4); C(2;-4).
Đúng 0
Bình luận (0)
Lập bảng biến thiên và vẽ đồ thị của các hàm số: y = 2x2 + x + 1
y = 2x2 + x + 1
+ Tập xác định: R
+ Đỉnh A(–1/4 ; 7/8).
+ Trục đối xứng x = –1/4.
+ Đồ thị không giao với trục hoành.
+ Giao điểm với trục tung B(0; 1).
Điểm đối xứng với B(0 ; 1) qua đường thẳng x = –1/4 là C(–1/2 ; 1)
+ Bảng biến thiên:
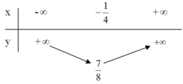
+ Đồ thị hàm số:
Đúng 0
Bình luận (0)
Cho hàm số y = 2 x 2 + 2 m x + m - 1 có đồ thị là C m , m là tham số.
Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m = -1
Với m = 1 ta được hàm số: y = 2 x 2 + 2 x
- TXĐ: D = R,
- Sự biến thiên:
+ Chiều biến thiên: y' = 4x + 2
y' = 0 ⇔ x = -1/2
+ Bảng biến thiên:
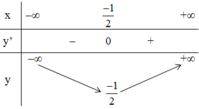
Kết luận: Hàm số nghịch biến trên (-∞; -1/2), đồng biến trên (-1/2; +∞).
Đồ thị hàm số có điểm cực tiểu là (-1/2; -1/2)
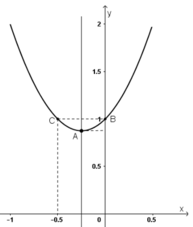
- Đồ thị:
Ta có: 2x2 + 2x = 0 ⇔ 2x(x + 1) = 0
QUẢNG CÁO⇒ x = 0; x = -1
+ Giao với Ox: (0; 0); (-1; 0)
+ Giao với Oy: (0; 0)
Đúng 0
Bình luận (0)
Xét sự biến thiên và vẽ đồ thị của hàm số y=|-3x+3|
(giúp em với mọi người ,gấp lắm ạ)
hàm số tăng trên khoảng [1;+\(\infty\))
Hàm số giảm trên khoảng(-\(\infty\);-1)
Đúng 0
Bình luận (0)
Cho hàm số y = 2 x 4 − 4 x 2 (1). Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1).
Tập xác định: D = R
y′=0 ⇔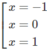 
Hàm số đồng biến trên mỗi khoảng (-1; 0) và (1; + ∞ )
Hàm số nghịch biến trên mỗi khoảng (− ∞ ; −1); (0; 1)
Hàm số đạt cực đại tại x = 0; y CĐ = 0
Hàm số đạt cực tiểu tại x = 1 hoặc x = -1; y CT = −2
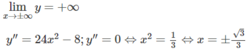
Đồ thị có hai điểm uốn:
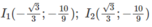
Bảng biến thiên:
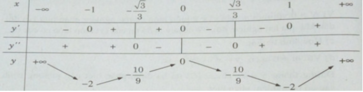
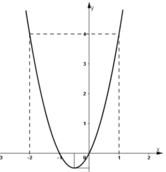
Đồ thị:
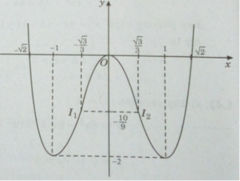
Đồ thị cắt trục hoành tại
Đúng 0
Bình luận (0)