Cho tam giác ABC có AB = 15 cm, AC = 21 cm. Lấy hai điểm M, N lần lượt trên hai cạnh AB, AC sao cho AM = 10 cm, AN = 14 cm. Chứng minh MN đi qua trọng tâm của tam giác ABC

Những câu hỏi liên quan
Cho tam giác ABC có AB = 15 cm, AC = 21 cm. Lấy hai điểm M, N lần lượt trên
hai cạnh AB, AC sao cho AM = 10 cm, AN = 14 cm. Chứng minh MN đi qua trọng tâm
của tam giác ABC.
Xét \(\Delta\)AMN và \(\Delta\)ABC có:
\(\frac{AM}{AB}=\frac{AN}{AC}\left(\frac{10}{15}=\frac{14}{21}\right)\)
=> MN // BC (1)
Gọi M là trung điểm của BC.
Gọi G là giao điểm AM và MN
Xét \(\Delta\)ABM có:
MG// BM ( theo(1))
=> \(\frac{AG}{AM}=\frac{AM}{AB}=\frac{10}{15}=\frac{2}{3}\)
=> G là trọng tâm của \(\Delta\)ABC
Vậy MN qua trong tâm \(\Delta\)ABC.
Cho tam giác ABC có AB=21 cm,AC=28cm, BC=35cm.
a, Chứng minh tam giác ABC vuông
b, Kẻ AH vuông góc với BC (H thuộc BC). Chứng minh AH^2=HB.HC
c, Trên cạnh AC và AB lần lượt lấy hai điểm M và N sao cho
CM= 1/3 AC;AN =1/3 AB
Xem chi tiết
a, theo pitago đảo: 212 +282=1225=352 suy ra tam giác ABC vuông
b,theo pitago
AH2=AB2-BH2=AC2-CH2 suy ra 2AH2=AB2+AC2-BH2-CH2
suy ra 2AH2=BC2-BH2-CH2 (Mà BC=BH+CH) suy ra 2AH2=2BHxCH
Cho tam giác ABC. Trên cạnh AB và AC lần lượt lấy 2 điểm M và N:
AM= 3 cm, BM= 2 cm, AN= 7.5 cm, NC= 5 cm
Đường trung tuyến AI của tam giác ABC cắt MN tại K, chứng minh K là trung điểm của MN
Cho tam giác ABC có AB3 cm ; AC 4,5 cm. Lấy điểm M trên cạnh AB sao cho AM 1 cm , lấy điểm N trên cạnh AC sao cho AN 1,5 cm. a) Chứng minh rằng MN // BC. b) Gọi I là trung điểm của MN , tia AI cắt BC tại K. +) CM dfrac{MI}{BK} dfrac{AI}{AK} +) CM K là trung điểm của BC .c) CM IK , MK và BN đồng quy tại một điểm .
Đọc tiếp
Cho tam giác ABC có AB=3 cm ; AC= 4,5 cm. Lấy điểm M trên cạnh AB sao cho AM = 1 cm , lấy điểm N trên cạnh AC sao cho AN = 1,5 cm.
a) Chứng minh rằng MN // BC.
b) Gọi I là trung điểm của MN , tia AI cắt BC tại K.
+) CM \(\dfrac{MI}{BK}\)= \(\dfrac{AI}{AK}\)
+) CM K là trung điểm của BC .
c) CM IK , MK và BN đồng quy tại một điểm .
tự vẽ hình
a, có AM/AB=1/3
mà AN/AC=1,5/4,5=1/3
=> AM/AB=AN/AC
=> MN//BC
b, Ta có MN//BC=> tam giác AMN đồng dạng tam giác ABC
=> <AMN= <ABC
Xét tam giác AMI và tam giác ABK
<AMI= <ABC (cmt)
<MAK chung
=> tam giác AMI đồng dạng tam giác ABK
MI/BK= AI/AK
Đúng 1
Bình luận (0)
Câu 1.Cho tam giác ABC có AB 24 cm, AC 30 cm. Trên cạnh AB và AC lần lượtlấy các điểm M và N sao cho AM 8 cm, AN 10 cm.1.Chứng minh MN//BC2. Tính MN biết BC 36 cmCâu 2. Cho tam giác ABC có AB 10 cm, AC 20 cm. Trên cạnh AC đặt đoạn thẳngAD 5 cm. Chứng minh ABD ACB [Câu 3. Cho tam giác ABC vuông tại A và phân giác AD (D ∈ BC). Biết AB 15 cm,AC 20 cm. Tính DB và DC.Câu 4.Cho tam giác ABC vuông tại A (AB AC) và đường cao AH.1. Chứng minh BA2 BH.BC.2. Tính độ dài cạnh AC khi biết AB 3...
Đọc tiếp
Câu 1.Cho tam giác ABC có AB = 24 cm, AC = 30 cm. Trên cạnh AB và AC lần lượt
lấy các điểm M và N sao cho AM = 8 cm, AN = 10 cm.
1.Chứng minh MN//BC
2. Tính MN biết BC = 36 cm
Câu 2. Cho tam giác ABC có AB = 10 cm, AC = 20 cm. Trên cạnh AC đặt đoạn thẳng
AD = 5 cm. Chứng minh ABD \= ACB [
Câu 3. Cho tam giác ABC vuông tại A và phân giác AD (D ∈ BC). Biết AB = 15 cm,
AC = 20 cm. Tính DB và DC.
Câu 4.Cho tam giác ABC vuông tại A (AB < AC) và đường cao AH.
1. Chứng minh BA2 = BH.BC.
2. Tính độ dài cạnh AC khi biết AB = 30 cm, AH = 24 cm.
3. Trên cạnh AC lấy điểm M sao cho CM = 10 cm, trên cạnh BC lấy điểm N sao cho CN
= 8 cm. Chứng minh tam giác CMN vuông.
4. Chứng minh CM.CA = CN.CB
Câu 5. (7đ) Cho tam giác ABC nhọn và đường cao AH. Kẻ HI ⊥ AB và HK ⊥ AC.
1. Chứng minh AH2 = AI.AB.
2. Chứng minh 4AIK v 4ACB
3. Đường phân giác của góc AHB cắt AB tại E. Biết EB/ AB = 2/ 5 . Tính tỉ số BI /AI
Câu 6. Cho tam giác AOB cân tại O (O <b 90◦
) và hai đường cao AD, BE. Đường vuông
góc với OA tại A cắt tia OB tại C. Chứng minh:
1. ED//AB.
2. OB2 = OE.OC
3. AB là đường phân giác của DAC \.
4. (Chứng minh BD.OA = BC.OE
giúp mình với nhé :( cần gấp
Tam giác ABC có độ dài các cạnh AB = 24cm, AC = 30cm, BC = 36cm. Trên cạnh AB lấy điểm M sao cho AM =20cm, trên cạnh AC lấy điểm N sao cho AN =16 cm. Chứng minh tam giác ANM đồng dạng với tam giác ABC và tính MN
Xét ΔANM và ΔABC có
AN/AB=AM/AC
\(\widehat{NAM}\) chung
Do đó: ΔANM\(\sim\)ΔABC
Đúng 0
Bình luận (1)
Cho tam giác ABC. trên cạnh AB và AC lần lượt lấy hai điểm M và N biết AM= 3 cm. AM Bằng 7,8 cm .NC = 5 cm a. Chứng minh rằng MN song song với BC b gọi I là điểm trên BC. K là giao điểm của AI và MN cho AC = 6 cm Tính KI
Cho tam giác ABC có AB = 15 cm, AC = 20 cm. Trên hai cạnh AB, AC lần lượt lấy 2 điểm E, D sao cho AD = 8cm, AE = 6cm. Chứng minh Δ AED ∼ Δ ABC.
Xét Δ AED và Δ ABC có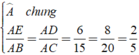
⇒ Δ AED ∼ Δ ABC ( c - g - c )
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 15 cm, AC = 20 cm. Trên hai cạnh AB, AC lần lượt lấy 2 điểm E, D sao cho AD = 8cm, AE = 6cm. Chứng minh Δ AED ∼ Δ ABC.
Xét Δ AED và Δ ABC có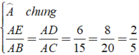
⇒ Δ AED ∼ Δ ABC ( c - g - c )
Đúng 0
Bình luận (0)

















