Để B nguyên thì 5n+1+6 chia hết cho 5n+1

=>\(5n+1\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)

mà n nguyên

nên \(n\in\left\{0;1\right\}\)

Đáp án cần chọn là: B

A = 3 n − 5 n + 4 = 3 n + 12 − 12 − 5 n + 4 = 3 n + 4 + − 17 n + 4 = 3 n + 4 n + 4 + − 17 n + 4 = 3 + − 17 n + 4

Vì n∈Z nên để A∈Z thì n + 4∈U(−17) = {±1;±17}

Ta có bảng:

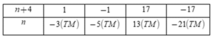
Vậy n∈{−21;−5;−3;13}

a)Để A có giá trị nguyên thì 3n+4 chia hết cho n-1

=>3(n-1)+7 chia hết cho n-1

=> n-1 thuộc Ư(7)={1;7;-1;-7}

Phần cuối bn tự làm nha

Còn câu b làm tương tự

a) Từ đề bài, ta có:

\(A=\frac{3n+4}{n-1}=\frac{3\left(n-1\right)+7}{n-1}=3+\frac{7}{n-1}\)

\(\Rightarrow\left(n-1\right)\inƯ\left(7\right)\)

\(\Rightarrow\left(n-1\right)\in\left\{\pm1;\pm7\right\}\)

\(\Rightarrow n\in\left\{2;0;-6;8\right\}\)

b) \(\frac{6n-3}{3n+1}=\frac{2\left(3n+1\right)+5}{3n+1}=2+\frac{5}{3n+1}\)

\(\Rightarrow\left(3n+1\right)\inƯ\left(5\right)\)

\(\Rightarrow\left(3n+1\right)\in\left\{\pm1;\pm5\right\}\)

\(\Rightarrow n\in\left\{\frac{-2}{3};0;-2;\frac{4}{3}\right\}\)

Tìm các giá trị nguyên của n để các phân số sau có giá trị là số nguyên

a)A=3n+4/n-1

b)6n-3/3n+1

a) Học sinh tự làm

b) 2 n + 1 n + 1 ( n ≠ − 1 ) có giá trị là số nguyên khi (2n +1) ⋮  (n +1) hay [2(n +1) -1] ⋮  (n +1)

Từ đó suy ra 1 ⋮  (n +1)

Do đó n ∈  {- 2;0).

Để 5n+1/3n+2 nhận giá trị nguyên

thì 5n+1 phải chia hết cho 3n+2

ta có:

5n+1 chia hết 3n+2

a. A có giá trị là số nguyên <=> n+5 chia hết cho n+9

<=>(n+9)-4 chia hết cho n+9

<=> 4 chia hết cho n+9 (vì n+9 chia hết cho n+9 )

<=> n+9 là ước của 4 

=> n+9 = 1,-1 , 2 ,-2,4,-4

sau đó bn tự tìm n ha 

b, B là số nguyên <=>3n-5 chia hết cho 3n-8

<=>(3n-8)+5 chia hết cho 3n-8

<=> 5 chia hết cho 3n-8

<=> 3n-8 là ước của 5 

=> 3n-8 =1,-1,5,-5

tiếp bn lm ha

c, D là số nguyên <=> 5n+1 chia hết cho 5n+4

<=> (5n+4)-3 chia hết cho 5n+4

<=> 3 chia hết cho 5n +4

<=> 5n +4 là ước của 3 

=> 5n+4 =1, -1,3,-3

 tiếp  theo bn vẫn tự lm ha 

đoạn tiếp theo ở cả 3 câu , bn tìm n theo từng trường hợp rồi xem xem giá trị n nào thỏa mãn n là số nguyên là OK . chúc bn học giỏi

a) A nguyên khi (12n + 17) ⋮ (3n + 1)

Ta có:

12n + 17 = 12n + 4 + 13

= 4(3n + 1) + 13

Để (12n + 17) ⋮ (3n + 1) thì 13 ⋮ (3n + 1)

⇒ 3n + 1 ∈ Ư(13) = {-13; -1; 1; 13}

⇒ 3n ∈ {-14; -2, 0; 12}

⇒ n ∈ {-14/3; -2/3; 0; 4}

Mà n là số nguyên

⇒ n ∈ {0; 4}

b) Để A là số nguyên thì ⋮ (10n + 9) (5n - 1)

Ta có:

10n + 9 = 10n - 2 + 11

= 2(5n - 1) + 11

Để (10n + 9) ⋮ (5n - 1) thì 11 ⋮ (5n - 1)

⇒ 5n - 1 ∈ Ư(11) = {-11; -1; 1; 11}

⇒ 5n ∈ {-10; 0; 2; 12}

⇒ n ∈ {-2; 0; 2/5; 12/5}

Mà n là số nguyên

⇒ n ∈ {-2; 0}

n = -6 ; 0 ; 2 ; 8

ta có : A=\(\frac{3n+4}{n-1}=\frac{3n-3+7}{n-1}=\frac{3\left(n-1\right)+7}{n-1}=3+\frac{7}{n-1}\)

để A thuộc Z => 3+ \(\frac{7}{n-1}\)phải thuộc Z => \(\frac{7}{n-1}\in Z\)hay n-1 thuộc ước của 7

bạn tự làm nốt nhé

a) \(A=\frac{3-n}{n+1}=\frac{4-1-n}{n+1}=\frac{4}{n+1}-1\inℤ\)mà \(n\inℤ\)suy ra \(n+1\inƯ\left(4\right)=\left\{-4,-2,-1,1,2,4\right\}\)

\(\Leftrightarrow n\in\left\{-5,-3,-2,0,1,3\right\}\).

b) \(B=\frac{6n+5}{3n+2}=\frac{6n+4+1}{3n+2}=2+\frac{1}{3n+2}\inℤ\)mà \(n\inℤ\)suy ra \(3n+2\inƯ\left(1\right)=\left\{-1,1\right\}\)

\(\Rightarrow n\in\left\{-1\right\}\)

c) \(C\inℤ\Rightarrow3C=\frac{6n+3}{3n+2}=\frac{6n+4-1}{3n+2}=2-\frac{1}{3n+2}\inℤ\) mà \(n\inℤ\)suy ra 

.\(3n+2\inƯ\left(1\right)=\left\{-1,1\right\}\)\(\Rightarrow n\in\left\{-1\right\}\)

Thử lại thỏa mãn.