Cho đoạn AB = 4a . Với điểm M tùy ý, tìm giá trị nhỏ nhất của tổng \(A=3MA^2+MB^2\)
Những câu hỏi liên quan
Cho đoạn AB = 4a . Với điểm M tùy ý, tìm giá trị nhỏ nhất của tổng \(A=3MA^2+MB^2\)
gg
Cho tam giác ABC vuong tại A có AB= 3; AC=4. Gọi I là trung điểm AC, d là đường trung trực của đoạn AC và M là điểm tùy ý trên d
a) Chứng minh rằng MA +MB > bằng 5
b) Xác định vị trí của M để tổng MA+MB nhỏ nhất. Tìm giá trị nhỏ nhất đó
Trong không gian Oxyz, cho bốn điểm A (3;1;0), B(2;0;-1), C(0;2;-1), D (0;0;2). Với mỗi điểm M tùy ý, đặt TMA+MB+MC+MD. Gọi
M
∘
a
;
b
;
c
sao cho T đạt giá trị nhỏ nhất. Lúc đó, tổng
a
+
5
b
+
c
bằng A. 3. B. -13. C. 7. D. 4
Đọc tiếp
Trong không gian Oxyz, cho bốn điểm A (3;1;0), B(2;0;-1), C(0;2;-1), D (0;0;2). Với mỗi điểm M tùy ý, đặt T=MA+MB+MC+MD. Gọi M ∘ a ; b ; c sao cho T đạt giá trị nhỏ nhất. Lúc đó, tổng a + 5 b + c bằng
A. 3.
B. -13.
C. 7.
D. 4
cho hình vuông ABCD có cạnh a. Gọi d là đường thẳng qua D và song song với AC. M là điểm tùy ý trên d. Giá trị nhỏ nhất của biểu thức\(T=\left|\overrightarrow{MA}+2\overrightarrow{MB}+3\overrightarrow{MC}\right|\)
Trong không gian với hệ tọa độ Oxyz, cho 4 điểm A(7;2;3), B(1;4;3), C(1;2;6), D(1;2;3) và điểm M tùy ý. Tính độ dài OM khi biểu thức
P
M
A
+
M
B
+
M
C
3
M
D
đạt giá trị nhỏ nhất:
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho 4 điểm A(7;2;3), B(1;4;3), C(1;2;6), D(1;2;3) và điểm M tùy ý. Tính độ dài OM khi biểu thức P = M A + M B + M C = 3 M D đạt giá trị nhỏ nhất:
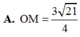
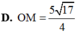
Cho tam giác ABC vuông tại A, BC=a\(\sqrt{2}\)Trên các cạnh BC, AB và AC lần lượt lấy các điểm M, D, E tùy ý. Tìm giá trị nhỏ nhất MD+ME. Giúp mk với nka các bn !!!
Cho tam giác A B C , M là điểm tùy ý trong mặt phẳng tam giác. Tìm giá trị nhỏ nhất biểu thức ∣ ∣ ∣ 2 −−→ M A + −−→ M B + −−→ M C ∣ ∣ ∣ + ∣ ∣ ∣ −−→ M B + −−→ M C ∣ ∣ ∣ ?
Bạn nên viết lại đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.
Đúng 2
Bình luận (0)
Cho (O;R) với dây AB cố định sao cho khoảng cách từ O tới AB bằng R/2. Gọi H là trung điểm của AB, tia HO cắt đường tròn (O;R) tại C. Trên cung nhỏ AB lấy điểm M tùy ý (M khác A, B). Đường thẳng qua A và song song với MB cắt CM tại I. Dây Cm cắt Ab tại K1. So sánh góc AIM vs góc ACB2. cm 1/MA + 1/MB 1/MK3. Gọi R1 R2 lần lượt là bán kính đường tròn ngoại tiếp tam giác MAK và tam giác MBK, hãy xác định vị trí của điểm M trên cung nhỏ Ab để thích R1xR2 đạt giá trị lớn nhất
Đọc tiếp
Cho (O;R) với dây AB cố định sao cho khoảng cách từ O tới AB bằng R/2. Gọi H là trung điểm của AB, tia HO cắt đường tròn (O;R) tại C. Trên cung nhỏ AB lấy điểm M tùy ý (M khác A, B). Đường thẳng qua A và song song với MB cắt CM tại I. Dây Cm cắt Ab tại K
1. So sánh góc AIM vs góc ACB
2. cm 1/MA + 1/MB = 1/MK
3. Gọi R1 R2 lần lượt là bán kính đường tròn ngoại tiếp tam giác MAK và tam giác MBK, hãy xác định vị trí của điểm M trên cung nhỏ Ab để thích R1xR2 đạt giá trị lớn nhất
Cho I là trung điểm đoạn thẳng AB, M là điểm tùy ý, H là hình chiếu của M trên AB. Chứng minh rằng:
a, \(\overrightarrow{MI}.\overrightarrow{AB}=\dfrac{1}{2}\left(MB^2-MA^2\right)\)