Cho ΔABC cân ở A, trung tuyến BM và CN cắt nhau ở G. I đối xứng với G qua N ; H đối xứng với G qua M. Chứng minh :
a) MNBC ; MNIH là hình thang cân.
b) BIHC là hình chữ nhật.
c) AIGH là hình thoi.
d) IH cắt AB ; AC ở P và Q. C/m IP = PQ = QH.
Những câu hỏi liên quan
Cho ΔABC cân ở A, trung tuyến BM và CN cắt nhau ở G. I đối xứng với G qua N ; H đối xứng với G qua M. Chứng minh :
a) MNBC ; MNIH là hình thang cân.
b) BIHC là hình chữ nhật.
c) AIGH là hình thoi.
d) IH cắt AB ; AC ở P và Q. C/m IP = PQ = QH.
Bài 2: Cho ΔABC cân tại A, các đường trung tuyến BM và CN cắt nhau tại G. Gọi D là điểm đối xứng với G qua M, E là điểm đối xứng với G qua N. Chứng minh BEDC là hình chữ nhật.
Xét tứ giác BCDE có
G là trung điểm của BD
G là trung điểm của CE
Do đó: BCDE là hình bình hành
mà \(\widehat{EBC}=90^0\)
nên BCDE là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì? Vì sao?
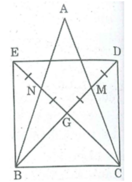
* Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G
Suy ra: G là trọng tâm của ∆ ABC .
⇒ GB = 2GM (tính chất đường trung tuyến)
GC = 2GN (tính chất đường trung tuyến)
Điểm D đối xứng với điểm G qua điểm M
⇒ MG = MD hay GD = 2GM
Suy ra: GB = GD (l)
Điểm E đối xứng với điểm G qua điểm N
⇒ NG = NE hay GE = 2GN
Suy ra: GC = GE (2)
Từ (1) và (2) suy ra tứ giác BCDE là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Xét ∆ BCM và ∆ CBN, có: BC cạnh chung
∠ (BCM) = ∠ (CBN) (tính chất tam giác cân)
CM = BN (vì AB = AC)
Suy ra: ∆ BCM = ∆ CBN (c.g.c)
⇒ ∠ (MBC) = ∠ (NCB) ⇒ ∆ GBC cân tại G ⇒ GB = GC ⇒ BD = CE
Hình bình hành BCDE có hai đường chéo bằng nhau nên nó là hình chữ nhật.
Đúng 0
Bình luận (0)
Cho tam giac ABC ,cac trung tuyến BM,CN cắt nhau tại G.gọi P là điểm đối xứng với M qua G,gọi Q là điểm đối xứng của N qua G.
a,tứ giác MNPQ là hình gì?
b,nếu tam giác ABC cân ở A thì MNPQ là hình gì?.Vì sao?
a) Vì BM là đường trung tuyến AC (gt)=>AM=CM
Vì CN là đường trung tuyến AB(gt)=>AN=BN
=>MN là đường trung bình tam giác ABC
=>MN//BC, MN=1/2 BC (điều1)
Ta lại có:
G là trung điểm MP(vì P là điểm đối xứng vs M qua G
=>PG=GM
VÌ GM=1/2 BG
PG=GM
=>BP=PG
Làm tương tự:GQ=CQ
Ta có:BP=PG(cmt)
GQ=CQ (cmt)
=>PQ là đường trung bình tam giác BGC
=>PQ//BC, PQ=1/2 BC (điều 2)
Từ 1 và 2 điều trên =>MN=PQ(cug=1/2 BC)
MN//PQ(cug //BC)
=>MNPQ lầ hình bình hành (t/c hbh )
b)Nếu tam giác ABC cân tại A thì AG vuông góc BC
=>PN vuông góc vs BC.Mặt khác PQ//BC
=>PN vuông góc vs PQ mà MNPQ là hình bình hành(cmt)
lại có 1 góc =90độ=>MNPQ là hình chữ nhật
Đúng 0
Bình luận (4)
Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì ? Vì sao ?
Cho tam giác ABC các trung tuyến BM;CN cắt nhau tại G gọi P là điểm đối xứng của M qua G ;gọi Q là điểm đối xứng của N qua G
tứ giác MNPQ la hình gì ?
NẾU tam giác ABC cân ở A thì tứ giác MNPQ là hình gì ?vì sao
Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điiểm đối xứng G qua M, E đối xứng G qua N. Tứ giác BEDC là hình gì? Vì sao?
Tự vẽ hình:
cminh:Vì D đối xứng với G qua M
=>GM=MD Hay GD=2GM
Vì BM;CN cắt nhau tại G trong tam giác ABC
=>G là trọng tâm trong Tam giác ABC =>BG=2GM
Suy ra : GD=BG(vì =2GM)=> G là trung điểm của BD (1)
Ta lại có : E đối xứng với G qua N=> EN=GN Hay EG=2NG
Và CG=2GN( G là trọng tâm)
Suy ra: CG=EG ( vì =2NG) (2) (*)
Từ (1) (2)=> Tứ giác BEDC là hình bình hành
Xét \(\Delta\)CBM Và \(\Delta\)BCN Có:
BC: Cạnh chung
Góc B=C(g/t)
BN=CM(AB=AC)
=> hai tam giác bằng nhau(c-g-c)
=>MBC=NCB(2 góc tương ứng) hay tam giác GBC cân=> BG=GC (**)
Từ (*) (**)=> Hình bình hành BEDC là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi
D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là
hình gì? Vì sao?
Cho tam giác ABC, các trung tuyến BM và CN cắt nhau ở G. Gọi P là điểm dối xứng của điểm M qua G. Gọi Q là điểm đối xứng của điểm N qua G.Tứ giác MNPQ là hình gì? Vì sao ?