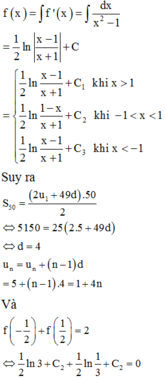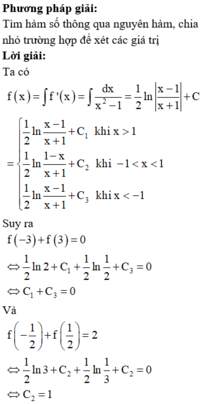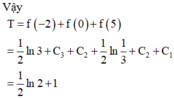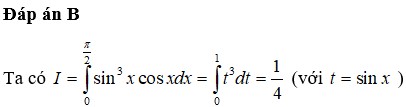cho hàm số f x là -15/x tính f5

Những câu hỏi liên quan
Cho hàm số
y
f
(
x
)
x
2
-
2
x
5
+
5
. Tính
f
5
-
3
. A.
2
5
-
3
B.
-
2...
Đọc tiếp
Cho hàm số y = f ( x ) = x 2 - 2 x 5 + 5 . Tính f 5 - 3 .
A. 2 5 - 3
B. - 2 5 + 3
C. 3
D. - 3
Ta có y = f x = ( x - 5 ) 2 = x - 5 nên
f 5 - 3 = 5 - 3 - 5 = - 3 = 3 .
Vậy đáp án là C.
Nhận xét: Học sinh có thể mắc sai lầm khi tính y = f x = x - 5 , từ đó dẫn đến việc tính f 5 - 3 = - 3 và chọn D. Hoặc tính nhầm thành y = f x = x + 5 sẽ dẫn đến f 5 - 3 = 2 5 - 3 , từ đó chọn A. Hoặc cũng có thể tính thành y = f x = - ( x + 5 ) , dẫn đến f 5 - 3 = - 2 5 + 3 . Đáp án là B.
Đúng 0
Bình luận (0)
Cho các hàm số f1(x)=x , f2(x)=-2x , f3(x)=1 , f4(x)=5 , f5(x)=1/x ,f6(x)=x^2
Trong các hàm số trên hàm số nào có tính chất f(-x)=-f(x)
NHANH NHA 4H 30 NỘP RỒI!
Cho hàm số f (x) có đạo hàm là
f
x
.
Đồ thị hàm số
y
f
x
được cho như hình bên. Biết rằng
f
0
+
f
3
f
2
+
f
5
.
Gía trị nhỏ nhất, giá trị lớn nhất của f (x) trên đoạn
0
;...
Đọc tiếp
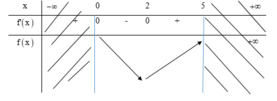
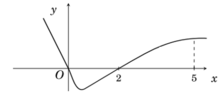
Cho hàm số f (x) có đạo hàm là f ' x . Đồ thị hàm số y = f ' x được cho như hình bên. Biết rằng f 0 + f 3 = f 2 + f 5 . Gía trị nhỏ nhất, giá trị lớn nhất của f (x) trên đoạn 0 ; 5 lần lượt là
A. f 2 , f 5
B. f 0 , f 5
C. f 2 , f 0
D. f 1 , f 5
Đáp án A
Lập được bảng biến thiên của hàm số như sau:
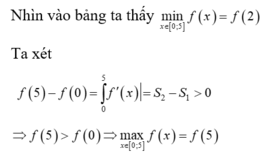
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
xác định trên
R
-
1
;
1
và thỏa mãn
f
(
x
)
1
x
2
-
1
. Biết
f
(
-
3
)
+...
Đọc tiếp
Cho hàm số f ( x ) xác định trên R \ - 1 ; 1 và thỏa mãn f ' ( x ) = 1 x 2 - 1 . Biết f ( - 3 ) + f ( 3 ) = 0 và f ( - 1 2 ) + f ( 1 2 ) = 2 . Tính T = f - 2 + f 0 + f 5
![]()
![]()
![]()
![]()
Cho hàm số f(x) có đạo hàm là
f
x
. Đồ thị của hàm số
y
f
x
được cho như hình vẽ bên. Biết rằng
f
0
+
f
3
f
2
+
f
5
. Giá trị nhỏ nhất và giá trị lớn nhất của f(x) trên đoạn
0
;
5...
Đọc tiếp
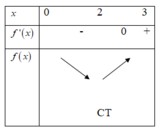
Cho hàm số f(x) có đạo hàm là f ' x . Đồ thị của hàm số y = f ' x được cho như hình vẽ bên. Biết rằng f 0 + f 3 = f 2 + f 5 . Giá trị nhỏ nhất và giá trị lớn nhất của f(x) trên đoạn 0 ; 5 lần lượt là

A. f 0 , f 5
B. f(2); f(0)
C. f(1); f(5)
D. f(2); f(5)
Đáp án D
Từ đồ thị y = f ' x trên đoạn 0 ; 5 , ta có bảng biến thiên của hàm số y = f x như hình vẽ bên
Suy ra min 0 ; 5 f x = f 2 . Từ giả thiết, ta có
f 0 + f 3 = f 2 + f 5 ⇔ f 5 − f 3 = f 0 − f 2
Hàm số f(x) đồng biến trên 2 ; 5
⇒ f 3 > f 2 ⇒ f 5 − f 2 > f 5 − f 3
= f 0 − f 2 ⇔ f 5 > f 0
Suy ra
max 0 ; 5 f x = f 0 , f 5 = f 5
Đúng 0
Bình luận (0)
Cho hàm số f(x) xác định trên
ℝ
−
1
;
1
và thỏa mãn
f
x
1
x
2
−
1
.
Biết
f
−
3
+
f
3
0...
Đọc tiếp
Cho hàm số f(x) xác định trên ℝ \ − 1 ; 1 và thỏa mãn f ' x = 1 x 2 − 1 . Biết f − 3 + f 3 = 0 và f − 1 2 + f 1 2 = 2. Tính T = f − 2 + f 0 + f 5
A. 1 2 ln 2 − 1
B. ln 2 + 1
C. 1 2 ln 2 + 1
D. ln 2 − 1
Cho hàm số y = f(x) có f ' x = 1 2 x − 1 và f 1 = 1 thì f 5 có giá trị bằng
A. ln2
B. n3
C. ln(2) + 1
D. ln(3) + 1
Đáp án D.
Ta có:
f ' x = 2 2 x − 1 ⇒ f x = ∫ f ' x d x = ∫ d x 2 x − 1 = 1 2 . l n 2 x − 1 + C .
Đúng 0
Bình luận (0)
cho hàm số y=f(x)=48-3x/15-x với x là số nguyên, x khác 15. Giá trị lớn nhất của hàm số f(x) đạt được khi x =
000000000000000000000000000255555555555555555555555555555555555555555555555555555
Đúng 0
Bình luận (0)
Cho hàm số F(x) là một nguyên hàm của hàm số
f
(
x
)
sin
3
x
cos
x
. Tính
I
F
(
π
2
)
-
F
(
0
)
A.
I
π
2
B.
I
1
4
C.
I...
Đọc tiếp
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = sin 3 x cos x . Tính I = F ( π 2 ) - F ( 0 )
A. I = π 2
B. I = 1 4
C. I = 3 π 2
D. I = 3 4