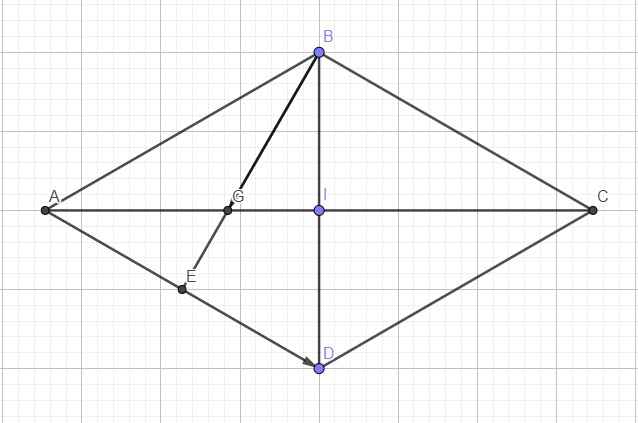
Cho hình thoi tâm có cạnh bằng 2a và góc ABC=120 độ . Gọi G là trọng tâm tam giác , tính độ dài của vectơ BG + AD

Những câu hỏi liên quan
Cho hình thoi ABCD tâm O có cạnh bằng 2a và góc ABC =120 độ. Gọi G là trọng tâm tam giác ABD, tính độ dài của vectơ BG + vectơ AD
Cho hình thoi ABCD tâm O có cạnh bằng 2a và góc ABC =120 độ. Gọi G là trọng tâm tam giác ABD, tính độ dài của vectơ BG + vectơ AD
\(\widehat{ABC}=120^0\Rightarrow\widehat{DAB}=180^0-120^0=60^0\)
\(\Rightarrow\Delta ABD\) đều
Gọi E là trung điểm AD \(\Rightarrow\overrightarrow{BE}=\dfrac{1}{2}\overrightarrow{BD}+\dfrac{1}{2}\overrightarrow{BA}\)
\(\Rightarrow\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BE}=\dfrac{1}{3}\overrightarrow{BD}+\dfrac{1}{3}\overrightarrow{BA}\)
\(\Rightarrow\overrightarrow{BG}+\overrightarrow{AD}=\dfrac{1}{3}\overrightarrow{BD}+\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{AD}=\dfrac{1}{3}\left(\overrightarrow{BA}+\overrightarrow{AD}\right)+\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{AD}\)
\(=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{4}{3}\overrightarrow{AD}=-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{4}{3}\overrightarrow{AD}\)
Đặt \(\overrightarrow{u}=\overrightarrow{BG}+\overrightarrow{AD}\Rightarrow\left|\overrightarrow{u}\right|^2=\left(-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{4}{3}\overrightarrow{AD}\right)=\dfrac{4}{9}AB^2+\dfrac{16}{9}AD^2-\dfrac{16}{9}\overrightarrow{AB}.\overrightarrow{AD}\)
\(=\dfrac{4}{9}.4a^2+\dfrac{16}{9}4a^2-\dfrac{16}{9}.2a.2a.cos60^0=\dfrac{16}{3}a^2\)
\(\Rightarrow\left|\overrightarrow{u}\right|=\dfrac{4a\sqrt{3}}{3}\)
Đúng 2
Bình luận (0)
cho tam giác ABC có 3 đường trung tuyến AD, BE, CF và trọng tâm G . gọi M là trung điểm BG . Đặt S1S1 là diện tích của tam giác có độ dài ba cạnh theo thứ tự bằng AD, BE, CF và S là diện tích tam giác ABC
a) tính SΔGDM theo S
b) c/m S1=3/4S
Bài 1: Cho hình thoi ABCD có cạnh a=30,1975 cm và góc ABC=60 độ . G là trọng tâm tam giác
ABC . Tính diện tích tứ giác AGCD
Bài 2: Cho tam giác ABC vuông tại A có AB=6,251 cm và góc B=56 độ .
a, Tính BC, AC và góc C
b, Tính độ dài đường cao AH và diện tích tam giác ABC
c, Tính độ dài đường trung tuyến AM và phân giác AD của tam giác ABC
Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC 12. Tính độ dài của vectơ
v
→
G
B
→
+
G
C
→
A.
v
→
2
B. ...
Đọc tiếp
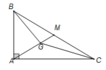
Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC= 12. Tính độ dài của vectơ v → = G B → + G C →
A. v → = 2
B. v → = 2 3
C. v → = 8
D. v → = 4
Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC 12. Tính độ dài của vectơ
v
→
G
B
→
+
G
C
→
.
Đọc tiếp
Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC = 12. Tính độ dài của vectơ v → = G B → + G C → .
![]()
![]()
![]()
![]()
Chọn D.
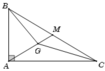
Gọi M là trung điểm của BC
Ta có ![]()
![]()
Mà AM = BC/ 2= 6 nên GA = 2/3. AM = 4
Đúng 0
Bình luận (0)
Cho hình thoi ABCD có cạnh bằng 5cm. Góc ABC=60 độ. G là trọng tâm của tam giác ABC. Tính diện tích hình tứ giác AGCD
Mn giúp mik vs. Bạn nào lm đúng mik tick cho
Trong mặt phẳng Oxy cho ba điểm A( 3;1) B(1;3) C(3;5)
a. tính vectơ AB vectơ BC vectơ AC
b. Tính độ dài ba cạnh của tam giác ABC Từ đó suy ra chu vi và diện tích của tam giác ABC
c. Tìm tọa độ trung điểm của các cạnh, trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp tam giác ABC
d. viết phương trình đường thẳng các cạnh AB, AC, BC, đường cao A,H trung tuyến BM
e. biết A,B,C lần lượt là trung điểm của các cạnh NM, MP, PN của tam giác NMP. viết phương trình tổng quát các cạnh của tam giác NMP.
Đọc tiếp
Trong mặt phẳng Oxy cho ba điểm A( 3;1) B(1;3) C(3;5)
a. tính vectơ AB vectơ BC vectơ AC
b. Tính độ dài ba cạnh của tam giác ABC Từ đó suy ra chu vi và diện tích của tam giác ABC
c. Tìm tọa độ trung điểm của các cạnh, trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp tam giác ABC
d. viết phương trình đường thẳng các cạnh AB, AC, BC, đường cao A,H trung tuyến BM
e. biết A,B,C lần lượt là trung điểm của các cạnh NM, MP, PN của tam giác NMP. viết phương trình tổng quát các cạnh của tam giác NMP.
Cho hình chóp tam giác S.ABC có
S
A
a
;
S
B
b
;
S
C
c
và
B
S
C
⏜
120
°
,
C
S
A
⏜
90...
Đọc tiếp
Cho hình chóp tam giác S.ABC có S A = a ; S B = b ; S C = c và B S C ⏜ = 120 ° , C S A ⏜ = 90 ° , A S B ⏜ = 60 ° . Gọi G là trọng tâm của tam giác ABC. Độ dài đoạn SG bằng
A. 1 3 a 2 + b 2 + c 2 + a b + b c + c a
B. a 2 + b 2 + c 2 + a b - b c
C. 1 3 a 2 + b 2 + c 2 + a b - c a
D. 1 3 a 2 + b 2 + c 2 + a b - b c
Chọn D.
Theo một kết quả cơ bản của hình học vectơ ta có
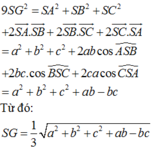
Đúng 0
Bình luận (0)