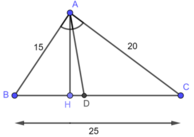
a) Trong tam giác ABC, ta có: AD là đường phân giác của:

Mà AB = 15cm và AC = 20cm ( gt )

Nên \(\dfrac{DC}{DB}\)

( Tính chất tỉ lệ thức đã học ở lớp 7 )

b) Kẻ 

Ta có:\(S_{ABD}\)=\(\dfrac{1}{2}\)AH.BD

\(S_{ACD}\)=\(\dfrac{1}{2}\)AH.CD

⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.CD}\)=\(\dfrac{BD}{DC}\)

Mà \(\dfrac{DB}{DC}\)=\(\dfrac{15}{12}\)=\(\dfrac{3}{4}\)

⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{3}{4}\)(đpcm)

a: Xét ΔABC có AD là phân giác

nên DB/AB=DC/AC

=>DB/DC=AB/AC=2/3

=>3DB-2DC=0

mà DB+DC=18

nên DB=7,2cm; DC=10,8cm

b: Xét ΔBDH vuông tại H và ΔCDK vuông tại K có

góc BDH=góc CDK

=>ΔBDH đồng dạng với ΔCDK

=>BH/CK=BD/CD=2/3

Hình tự vẽ lấy nhé

a) Trong tam giác ABC, ta có: AD là đường phân giác của:

\(\Rightarrow\frac{DB}{DC}=\frac{AB}{AC}\)

Mà AB = 15cm và AC = 20cm ( gt )

Nên \(\frac{DB}{DC}=\frac{15}{20}\)

\(\Rightarrow\frac{DB}{DB+DC}=\frac{15}{15+20}\)( Tính chất tỉ lệ thức đã học ở lớp 7 )

\(\Rightarrow\frac{DB}{BC}=\frac{15}{35}\Rightarrow DB=\frac{15}{35}.BC=\frac{15}{35}.25=\frac{75}{7}\left(cm\right)\)

b) Kẻ \(AH\perp BC\)

Ta có: \(S_{ABD}=\frac{1}{2}AH.BD\)

\(S_{ACD}=\frac{1}{2}AH.CD\)

\(\Rightarrow\frac{S_{ABD}}{S_{ACD}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.CD}=\frac{BD}{DC}\)

Mà \(\frac{DB}{DC}=\frac{15}{12}=\frac{3}{4}\)

\(\Rightarrow\frac{S_{ABD}}{S_{ACD}}=\frac{3}{4}\left(đpcm\right)\)

a, tam giác ABC vuông tại B có góc A = 30 độ => AC = 2 BC = 2. 3 = 6 cm

theo định lí Pytago ta có AB = \(\sqrt{ÃC^2-BC^2}=\sqrt{6^2-3^2}\) = \(3\sqrt{3}\) cm

góc C = 90 - 30 = 60 độ

b, tam giác ABH vuông tại H có góc A = 30 độ => AB = 2 BH => BH = \(\frac{3\sqrt{3}}{2}\)cm

theo định lí Pytago ta có AH = \(\sqrt{AB^2-BH^2}=\sqrt{\left(3\sqrt{3}\right)^2-\left(\frac{3\sqrt{3}}{2}\right)^2}=4,5cm\)

diện tích tam giác ABH =\(\frac{1}{2}.BH.AH=\frac{1}{2}.\frac{3\sqrt{3}}{2}.4,5=\frac{27\sqrt{3}}{8}\)cm vuông

mk bận quá k lm kịp 2 câu còn lại thông cảm nha 

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)

nên ΔABC vuông tại A

c: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot4.5}{2}=3\cdot4.5=13.5\left(cm^2\right)\)

a) Xét tam giác ABC có:

BD là tia phân giác \(\widehat{BAC}\)

\(\Rightarrow\dfrac{AB}{AC}=\dfrac{BD}{DC}=\dfrac{15}{20}=\dfrac{3}{4}\)(tính chất)

 \(\Rightarrow\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{BC}{7}=\dfrac{25}{7}\)(tính chất dãy tỉ số bằng nhau)

\(\Rightarrow\left\{{}\begin{matrix}DB=\dfrac{25.3}{7}=\dfrac{75}{7}\left(cm\right)\\DC=\dfrac{25.4}{7}=\dfrac{100}{7}\left(cm\right)\end{matrix}\right.\)

b) Kẻ đường cao AH của tam giác ABC

\(\Rightarrow\dfrac{S_{ACD}}{S_{ABC}}=\dfrac{\dfrac{1}{2}.AH.DC}{\dfrac{1}{2}.AH.BC}=\dfrac{DC}{BC}=\dfrac{100}{7}:25=\dfrac{4}{7}\)

a: Xét ΔABC có 

AD là đường phân giác ứng với cạnh BC

nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)

hay \(\dfrac{BD}{15}=\dfrac{CD}{20}\)

mà BD+CD=25cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{BD}{15}=\dfrac{CD}{20}=\dfrac{25}{35}=\dfrac{5}{7}\)

Do đó: \(BD=\dfrac{75}{7}cm;CD=\dfrac{100}{7}cm\)