Cho hình thang cân ABCD, đường cao AH. Goi E,F theo thứ tự là trung điểm của các cạnh bên AD và BC. Chứng minh rẳng EFCH là hình bình hành

Những câu hỏi liên quan
Cho hình thang cân ABCD, đường cao AH. Goi E,F theo thứ tự là trung điểm của các cạnh bên AD và BC. Chứng minh rẳng EFCH là hình bình hành
Cho hình thang cân ABCD, đường cao AH. Gọi E, F theo thứ tự là trung điểm của các cạnh bên AD, BC. Chứng minh rằng EFCH là hình bình hành.
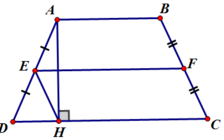
*Có AH ⊥ CD ⇒ ∆ AHD vuông tại H
E là trung điểm của AD ⇒ HE là trung tuyến ứng với cạnh huyền AD
⇒ HE = 1/2 AD (1)
*F là trung điểm của BC ⇒ CF = 1/2 BC (2)
Mà ABCD là hình thang cân ⇒ BC = AD (3)
Từ (1), (2) và (3) ta có: HE = CF (*)
*Mặt khác: EH = ED = 1/2 AD (Chứng minh trên)
⇒ ∆ EHD cân tại E
⇒ ∠ (EHD) = ∠ (EDH)
Mà ∠ (EDH) = ∠ (FCH) (góc đáy hình thang cân)
⇒ ∠ (FCH) = ∠ (EHD) (cùng bằng ∠ (EDH))
⇒EH // FC (2 góc ở vị trí đồng vị bằng nhau) (**)
Từ (*) và (**) ⇒ EFCH là hình bình hành (1 cặp cạnh song song và bằng nhau)
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD, đường cao AH. Gọi E, F theo thứ tự là trung điểm của các cạnh bên AD, BC. Chứng minh rằng EFCH là hình bình hành ?
chi hình thang ABCD đường cao AH gọi E và F thứ tự là trung điểm của AD và BC. Chứng minh EFCH là hình bình hành
cho hình thang Cân ABCD đường cao AH.Gọi E,F theo thứ tụ là trung điểm của các cạnh bên AD,BC.Chứng minh rằng:EFCH là hình bình hành
Bài 7: Cho hình thang cân ABCD (AB//CD ) , DC là đáy lớn AH là đường cao , M; N là trung điểm hai cạnh bên AD và BC . a) Chứng minh MNCH là hình bình hành b) Nếu AH=5cm . Tính đường trung bình của hình thang ABCD trên
1. Cho hình chữ nhật ABCD. Gọi E là chân đường vuông góc kẽ từ B đến Ac, I là trung điểm của AE, M là trung điểm của CD.
A, Gọi H là trung điểm của Be. cm: CH // IM.
B, Tính số đo góc BIM
2, Cho hình thang cân ABCD, đường cao AH. Gọi E,F theo thứ tự là trung điểm các cạnh bên AD,BC. c/ m: E,F,C
1. Cho hình chữ nhật ABCD. Gọi E là chân đường vuông góc kẽ từ B đến Ac, I là trung điểm của AE, M là trung điểm của CD.
A, Gọi H là trung điểm của Be. cm: CH // IM.
B, Tính số đo góc BIM
2, Cho hình thang cân ABCD, đường cao AH. Gọi E,F theo thứ tự là trung điểm các cạnh bên AD,BC. c/ m: E,F,C
Gọi M, N theo thứ tự là các trung điểm của hai đáy AD và BC của hình thang ABCD. Từ điểm O tùy ý thuộc đoạn MN, kẻ đường thẳng song song với đáy hình thang, đường thẳng này cắt các cạnh bên tại E và F. Chứng minh rằng O là trung điểm của EF.
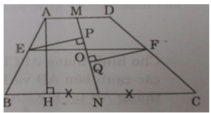
Ta có MA = MD, NC = NB (gt) và AD // BC.
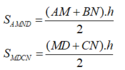
⇒ SAMND = SMCDN (các hình thang có các đáy bằng nhau và chung đường cao)
Do EF // AD nên đường cao từ E và F xuống AD bằng nhau, lại có AM = DM
⇒ SAEM = SDFM
Tương tự SBEN = SNFC
⇒ SAMNB - (SAEM + SBEN) = SDMNC - (SBEN + SNFC)
hay SEMN = SFMN
Hai tam giác trên có chung cạnh MN nên đường cao tương ứng bằng nhau hay EP = FQ
Xét ΔEPO và ΔFQO có:
∠EOP = ∠QOF (đối đỉnh)
EP = PQ (cmt)
∠EPO = ∠FQO = 90o
Do đó ΔEPO = ΔFQO (ch–gn) ⇒ OE = OF hay O là trung điểm của EF.
Đúng 0
Bình luận (0)















