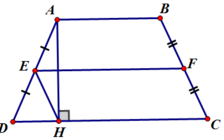
*Có AH ⊥ CD ⇒ ∆ AHD vuông tại H
E là trung điểm của AD ⇒ HE là trung tuyến ứng với cạnh huyền AD
⇒ HE = 1/2 AD (1)
*F là trung điểm của BC ⇒ CF = 1/2 BC (2)
Mà ABCD là hình thang cân ⇒ BC = AD (3)
Từ (1), (2) và (3) ta có: HE = CF (*)
*Mặt khác: EH = ED = 1/2 AD (Chứng minh trên)
⇒ ∆ EHD cân tại E
⇒ ∠ (EHD) = ∠ (EDH)
Mà ∠ (EDH) = ∠ (FCH) (góc đáy hình thang cân)
⇒ ∠ (FCH) = ∠ (EHD) (cùng bằng ∠ (EDH))
⇒EH // FC (2 góc ở vị trí đồng vị bằng nhau) (**)
Từ (*) và (**) ⇒ EFCH là hình bình hành (1 cặp cạnh song song và bằng nhau)










