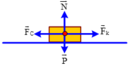
Một ô tô có khối lượng 1,5 tấn, khởi hành với gia tốc 0,3 m/s2. Khi ô tô có chở hàng hóa thì khởi hàng với gia tốc 0,2 m/s2. Hãy tính khối lượng của hàng hóa. Biết hợp lực tác dụng vào ô tô trong hai trường hợp đều bằng nhau

Những câu hỏi liên quan
Một xe tải chở hàng có tổng khối lượng xe và hàng hóa là 4 tấn, khởi hành với gia tốc
0
,
3
m
/
s
2
. Khi không chở hàng xe tải khởi hành với gia tốc
0
,
6
m
/
s
2
. Biết rằng hợp lực tác dụng lên ô tô trong hai trường hợp đều bằng nhau. Khối lượng của xe lúc không chở hàng hóa là A. 1 tấn. B. 1,5 tấn. C. 2 t...
Đọc tiếp
Một xe tải chở hàng có tổng khối lượng xe và hàng hóa là 4 tấn, khởi hành với gia tốc 0 , 3 m / s 2 . Khi không chở hàng xe tải khởi hành với gia tốc 0 , 6 m / s 2 . Biết rằng hợp lực tác dụng lên ô tô trong hai trường hợp đều bằng nhau. Khối lượng của xe lúc không chở hàng hóa là
A. 1 tấn.
B. 1,5 tấn.
C. 2 tấn.
D. 2,5 tấn.
Một xe tải chở hàng có tổng khối lượng xe và hàng là 4 tấn, khởi hành với gia tốc
0
,
3
m
/
s
2
.Khi không chở hàng xe tải khởi hành với gia tốc
0
,
6
m
/
s
2
.Biết rằng lực tác dụng vào ô tô trong hai trường hợp đều bằng nhau. Khối lượng của xe lúc không chở hàng là A. 1,0 tấn B. 1,5 tấn. C. 2,0 tấn. D. 2...
Đọc tiếp
Một xe tải chở hàng có tổng khối lượng xe và hàng là 4 tấn, khởi hành với gia tốc 0 , 3 m / s 2 .Khi không chở hàng xe tải khởi hành với gia tốc 0 , 6 m / s 2 .Biết rằng lực tác dụng vào ô tô trong hai trường hợp đều bằng nhau. Khối lượng của xe lúc không chở hàng là
A. 1,0 tấn
B. 1,5 tấn.
C. 2,0 tấn.
D. 2,5 tấn.
Đáp án C
Lực tác dụng trong hai trường hợp bằng nhau nên:
F = m 1 a 1 = m 2 a 2 ⇒ 4.0 , 3 = m 2 .0 , 6 ⇒ m 2 = 2 t ấ n
Đúng 0
Bình luận (0)
Một xe tải chở hàng có tổng khối lượng xe và hàng là 4 tấn, khởi hành với gia tốc 0,3 m/s2. Khi không chở hàng xe tải khởi hành với gia tốc 0,6 m/s2. Biết rằng lực tác dụng vào ô tô trong hai trường hợp đều bằng nhau. Khối lượng của xe lúc không chở hàng là: A. 1,0 tấn. B. 1,5 tấn. C. 2,0 tấn. D. 2,5 tấn.
Đọc tiếp
Một xe tải chở hàng có tổng khối lượng xe và hàng là 4 tấn, khởi hành với gia tốc 0,3 m/s2. Khi không chở hàng xe tải khởi hành với gia tốc 0,6 m/s2. Biết rằng lực tác dụng vào ô tô trong hai trường hợp đều bằng nhau. Khối lượng của xe lúc không chở hàng là:
A. 1,0 tấn.
B. 1,5 tấn.
C. 2,0 tấn.
D. 2,5 tấn.
Chọn đáp án C
Lực tác dụng trong hai trường hợp bằng nhau nên:
F = m1a1 = m2a2
→ 4.0,3 = m2.0,6
→ m2 = 2 (tấn)
Đúng 0
Bình luận (0)
Một ô tô chuyển động trên đường ngang có khối lượng 1,5 tấn, khởi hành với gia tốc 0,3m/s^2. Khi ô tô có chở hành hóa thì khởi hành với gia tốc 0,2m/s^2. Biết hợp lực tác dụng vào ô tô trong hai trường hợp đều bằng nhau.a) Hãy tính khối lượng của hàng hóa?b) Coi hệ số ma sát lăn giữa bánh xe và mặt đường là 0,1; g9,8 m/s^2. Tính lực phát động Fk của đọng cơ xe khi xe không chở hàng?
Đọc tiếp
Một ô tô chuyển động trên đường ngang có khối lượng 1,5 tấn, khởi hành với gia tốc 0,3m/\(s^2\). Khi ô tô có chở hành hóa thì khởi hành với gia tốc 0,2m/\(s^2\). Biết hợp lực tác dụng vào ô tô trong hai trường hợp đều bằng nhau.
a) Hãy tính khối lượng của hàng hóa?
b) Coi hệ số ma sát lăn giữa bánh xe và mặt đường là 0,1; g=9,8 m/\(s^2\). Tính lực phát động Fk của đọng cơ xe khi xe không chở hàng?
Một ô tô chuyển động trên đường ngang có khối lượng 1,5 tấn, khỏi hành với gia tốc 0,3m/s^2. Khi ô tô có chỏ hành hóa tì khỏi hành với gia tốc 0,2m/s^2. Biết hợp lực tác dụng vào ô tô trong hai trường hợp đều bằng nhau.a) Hãy tính khối lượng của hàng hóa?b) Coi hệ số ma sát lăn giữa bánh xe và mặt đường là 0,1; g9,8 m/s^2. Tính lực phát đọng Fk của đọng cơ xe khi xe không chở hàng?
Đọc tiếp
Một ô tô chuyển động trên đường ngang có khối lượng 1,5 tấn, khỏi hành với gia tốc 0,3m/\(s^2\). Khi ô tô có chỏ hành hóa tì khỏi hành với gia tốc 0,2m/\(s^2\). Biết hợp lực tác dụng vào ô tô trong hai trường hợp đều bằng nhau.
a) Hãy tính khối lượng của hàng hóa?
b) Coi hệ số ma sát lăn giữa bánh xe và mặt đường là 0,1; g=9,8 m/\(s^2\). Tính lực phát đọng Fk của đọng cơ xe khi xe không chở hàng?
a) Gọi m là khối lượng hàng hóa trên xe.
Theo đề bài, ta có: \(F=0,3\times1500=450N\)
lại có \(F=0,2\times\left(m+1500\right)\)= 450
giải phương trình trên, ta được m = 750 kg
==> Vậy khối lượng hàng hóa trên xe là 750 kg
Đúng 0
Bình luận (0)
Một ô tô khối lượng 900 kg khởi hành từ trạng thái nghỉ có gia tốc không đổi là 3,5 m/s2. Tính động lượng của ô tô sau khi nó đi được quãng đường 40 m.
Vật khởi hành từ trạng thái nghỉ nên vận tốc ban đầu v0 = 0.
Vận tốc của ô tô khi đi được quãng đường 40 m là: \(v = \sqrt {2as} = \sqrt {2.3,5.40} = 2\sqrt {70} (m/s)\)
Động lượng của ô tô là: \(p = m.v = 900.2\sqrt {70} \approx 15060(kg.m/s)\)
Đúng 0
Bình luận (0)
Cho một ô tô khởi hành rời bến chuyển động nhanh dần đều sau khi đi được đoạn đường 100m có vận tốc ô tô khởi hành rời bến chuyển động nhanh dần đều sau khi đi được đoạn đường 100m có vận tốc 36km/h. Biết khối lượng của xe là 1000kg và
g
10
m
/
s
2
. Cho lực cản bằng trọng lực xe. Tính lực phát động vào xe. A. 1200N B. 1300N C. 1400N D. 1500N
Đọc tiếp
Cho một ô tô khởi hành rời bến chuyển động nhanh dần đều sau khi đi được đoạn đường 100m có vận tốc ô tô khởi hành rời bến chuyển động nhanh dần đều sau khi đi được đoạn đường 100m có vận tốc 36km/h. Biết khối lượng của xe là 1000kg và g = 10 m / s 2 . Cho lực cản bằng trọng lực xe. Tính lực phát động vào xe.
A. 1200N
B. 1300N
C. 1400N
D. 1500N
Một ô tô khối lượng 5 tấn, sau khi khởi hành 10s đi được quãng đường 50m. Biết lực cản tác dụng vào ô tô luôn bằng 1000N. Tính:
a) Lực kéo của động cơ xe.
b) Tốc độ và quãng đường xe đi được sau 20s.
c) Muốn xe sau khi khởi hành 10m đạt tốc độ 10m/s thì lực kéo của động cơ phải có giá trị như thế nào?
Một ô tô khối lượng 5 tấn, sau khi khởi hành 10s đi được quãng đường 50m. Biết lực cản tác dụng vào ô tô luôn bằng 1000N. Tính:
a) Lực kéo của động cơ xe.
b) Tốc độ và quãng đường xe đi được sau 20s.
c) Muốn xe sau khi khởi hành 10m đạt tốc độ 10m/s thì lực kéo của động cơ phải có giá trị như thế nào?
Chọn mốc thời gian lúc xe bắt đầu xuất phát, chiều dương là chiều chuyển động của xe.
a. Ta có \(s_1=v_ot+\dfrac{1}{2}at_1^2\) \(\Leftrightarrow50=0+\dfrac{1}{2}a.10^2\) \(\Leftrightarrow a=1\) (m/s^2)
\(F=ma=5000.1=5000\left(N\right)\)
\(F_k=F+F_c=5000+1000=6000\left(N\right)\)
b. \(v_2=v_0+at_2\) \(\Leftrightarrow\) \(v_2=20\) (m/s)
\(s_2=\dfrac{1}{2}at_2^2=\dfrac{1}{2}.1.20^2=200\left(m\right)\)
c. \(v_3^2-v_0^2=2a_3s_3\) \(\Leftrightarrow10^2-0=2.10.a_3\) \(\Leftrightarrow a_3=5\) (m/s^2)
\(F_3=ma_3=5000.5=25000\left(N\right)\)
\(F_{k3}=25000+1000=26000\left(N\right)\)
Đúng 9
Bình luận (3)