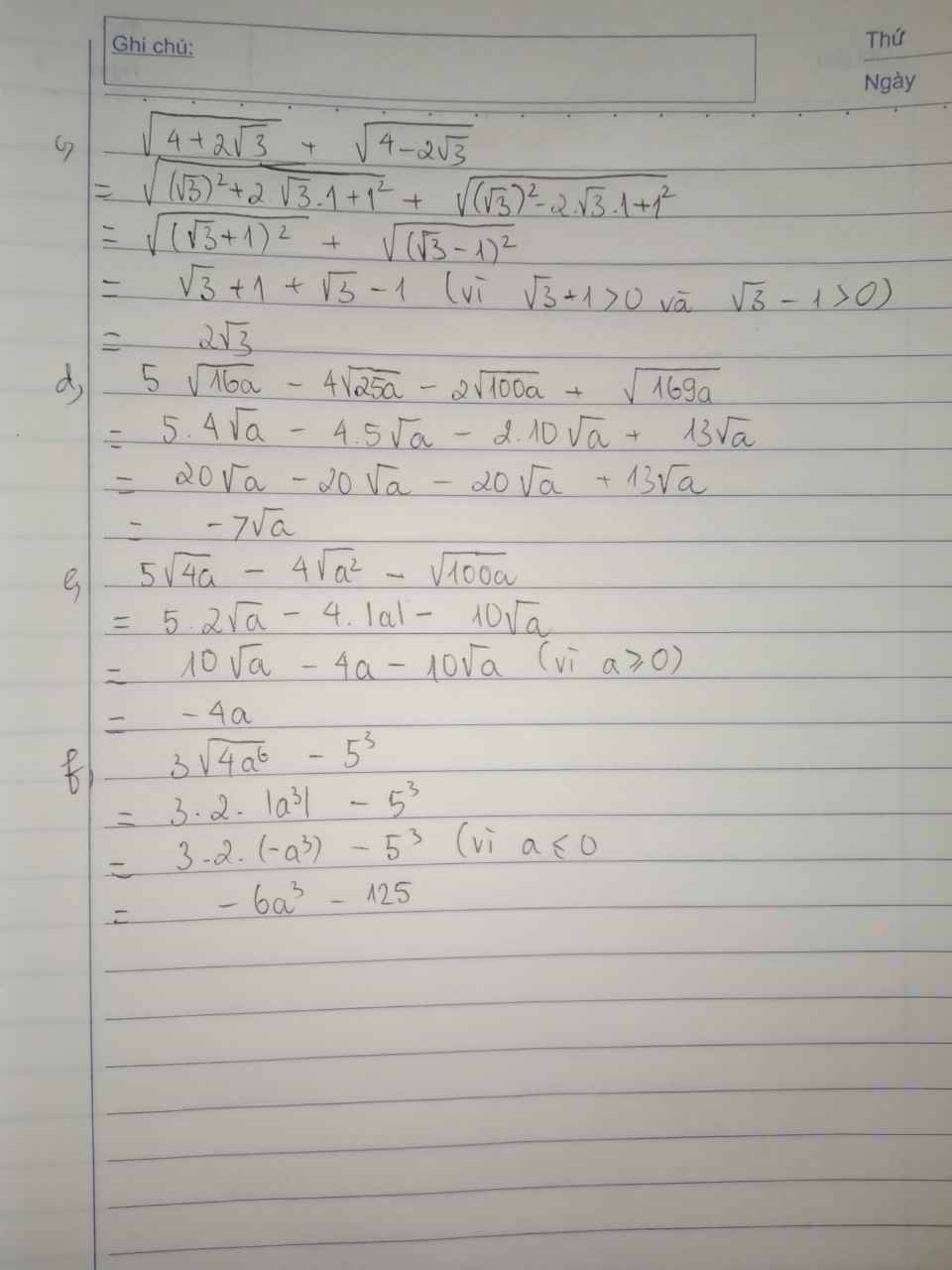cmr: gt biểu thức P=a^4-4a^3+5a^2-4a+5>0 với mọi a

Những câu hỏi liên quan
CMR :
a) x^2 - 20x +101 >0 với mọi x
b) 4a^2 + 4a + 2 >0 với mọi a
c) (x+2) (x+4) (x+6) (x+8) + 16 >0 với mọi x,y
Giúp mình với mình cần gấp lắm !!
a) Ta có: \(x^2-20x+101=x^2-2.x.10+10^2+1=\left(x-10\right)^2+1\)
Vì \(\left(x-10\right)^2\ge0\left(\forall x\in Z\right)\)
\(\Rightarrow\left(x-10\right)^2+1>1>0\)
Vậy x2-20x+101 >0 với mọi x
b) \(4a^2+4a+2=\left(2a\right)^2+2.2a.1+1+1=\left(2a+1\right)^2+1\)
Vì \(\left(2a+1\right)^2\ge0\left(\forall a\in Z\right)\)
\(\Rightarrow\left(2a+1\right)^2+1>1>0\)
Vậy 4a2+4a+2 > 0 với mọi a
c) \(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)+16\)
\(=\left(x+2\right)\left(x+8\right)\left(x+4\right)\left(x+6\right)+16\)
\(=\left(x^2+10x+16\right)\left(x^2+10x+24\right)+16\)
\(=\left(x^2+10x+16\right)\left(x^2+10x+16+8\right)+16\)
\(=\left(x^2+10x+16\right)^2+8\left(x^2+10x+16\right)+16\)
\(=\left(x^2+10x+20\right)^2\) \(\ge0\left(\forall x\right)\)
Đúng 0
Bình luận (0)
cho 5a2+2b2=11ab với a>b/5>0
tính giá trị của biểu thức A=(4a2-5b2)/(a2+3ab)
Cmr : a) x^2 - x + 1 > 0 với mọi x
b) 4a - 4a^2 -9 < 0 với mọi a
Cho biểu thức: A=[(16−a)a/(a2−4)+(2a+3)/(2−a)−(2−3a)/(a+2)]∶(a2+1)/(a3+4a2+4a)+1/(a2+1)
a) Rút gọn A
b) Tính giá trị của A khi a thỏa mãn a2 + 5a + 4 = 0
c) Chứng tỏ rằng A luôn không âm với mọi a thỏa mãn điều kiện xác định
cho a,b thỏa mãn 5a^2+2b^2=11ab và a>2b>0. tính giá trị biểu thức A=4a^2-5b^2/a^2+2ab
Lời giải:
$5a^2+2b^2=11ab$
$\Leftrightarrow 5a^2+2b^2-11ab=0$
$\Leftrightarrow (5a^2-10ab)-(ab-2b^2)=0$
$\Leftrightarrow 5a(a-2b)-b(a-2b)=0$
$\Leftrightarrow (a-2b)(5a-b)=0$
Do $a>2b>0$ nên $a-2b>0$. Do dó $5a-b=0$
$\Leftrightarrow b=5a$. Khi đó:
$A=\frac{4a^2-5b^2}{a^2+2ab}=\frac{4a^2-5(5a)^2}{a^2+2a.5a}=\frac{-121a^2}{11a^2}=-11$
Đúng 2
Bình luận (0)
rút gọn các biểu thức sau
c,\(\sqrt{4+2\sqrt{3}}+\sqrt{4-2\sqrt{3}}\) d,\(5\sqrt{16a}-4\sqrt{25a}-2\sqrt{100a}+\sqrt{169a}\) với a ≥ 0
e,\(5\sqrt{4a}-4\sqrt{a^2}-\sqrt{100a}\) với a ≥ 0 f,\(3\sqrt{4a^6}-5^3\) với a ≤ 0
chứng minh 4a^2+b^2-4a+2b+5/2>0 với mọi a,b
= (4a^2 -4a + 1) + (b^2 + 2b+ 1) + 1/2
= (2a-1)^2 + (b+1)^2 + 1/2 >0 với mọi a, b
Đúng 0
Bình luận (0)
Chứng minh các bất đẳng thức sau đây:
a) a4+b4+c4+1 >= 2a(b+c)
b) 4a4-4a3+5a2+2a+1 >= 0
c) (ab+bc+ca)2 >= 3abc(a+b+c)
Thanks
Chứng minh các bất đẳng thức sau đây:
a) a4+b4+c4+1 >= 2a(b+c)
b) 4a4-4a3+5a2+2a+1 >= 0
c) (ab+bc+ca)2 >= 3abc(a+b+c)
Thanks