Do (d1) song song với đường thẳng y = 2x nên a = 2

(d1): y = 2x + b

Thay tọa độ điểm (1; -1) vào (d) ta được:

2.1 + b = -1

⇔ b = -1 - 2

⇔ b = -3

Vậy (d1): y = 2x - 3

b) x = 0 ⇒ y = -3

*) Đồ thị:

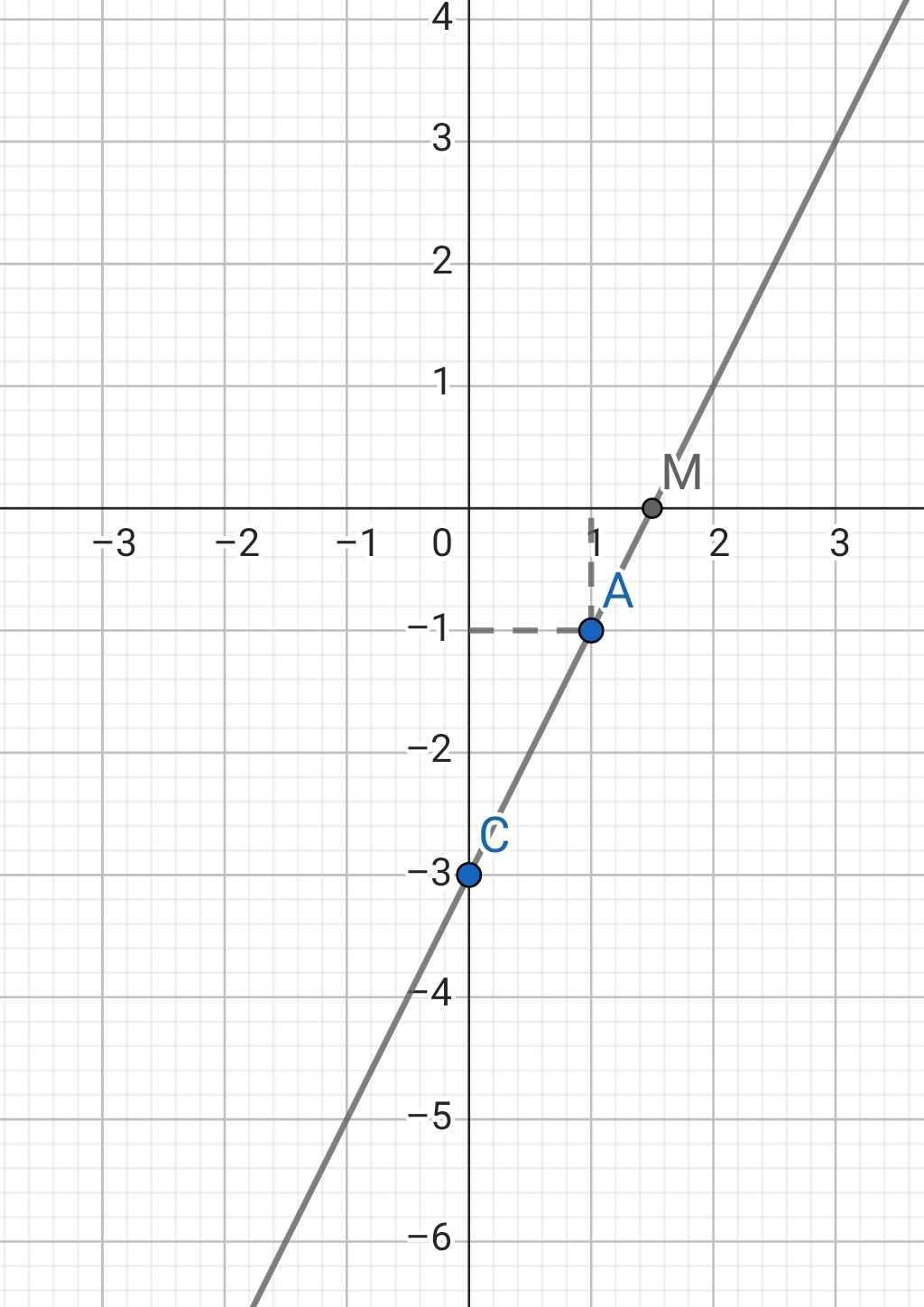
c) Phương trình hoành độ giao điểm của (d1) và (d2):

2x - 3 = 1/2 x + 1

⇔ 2x - 1/2 x = 1 + 3

⇔ 3/2 x = 4

⇔ x = 4 : 2/3

⇔ x = 8/3

⇒ y = 2.8/3 - 3 = 7/3

Vậy tọa độ giao điểm của (d1) và (d2) là (8/3; 7/3)

d) Ta có:

Gọi a là góc cần tính

⇒ tan(a) = 2

⇒ a ≈ 63⁰

(b) và (d) bạn tự xem kiến thức vẽ rồi áp dụng công thức tan là làm được nha=)

a)

Đồ thị hàm số (d₁)// đường thẳng `y=2x`

=> \(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b\ne0\end{matrix}\right.\)

=> `y=2x+b`

Do hàm số `y=2x+b` đi qua điểm `(1;-1)` nên `x=1`, `y=-1`:

`-1=2.1+b`

=> `b=-3`

Vậy hàm số `y=ax+b` là `y=2x-3`

c)

Ta có PTHĐGĐ giữa `d_1` và `d_2`:

 \(2x-3=\dfrac{1}{2}x+1\\ \Rightarrow x=\dfrac{8}{3}\Rightarrow y=\dfrac{7}{3}\)

Vậy `E=`\(\left(\dfrac{8}{3};\dfrac{7}{3}\right)\)

$HaNa$

Sorry, mk chưa học đồ thị bn ơi, đừng giận nha Huyền Anh Kute

bn ns gì trong hộp tin nhắn vậy, mk ko thấy vì bị quảng cáo che mất rồi Huyền Anh Kute

??????????

a) \(\hept{\begin{cases}x=1\\y=3\end{cases}\Rightarrow3=a.1\Rightarrow a=3}\)

b) B(x_o,y_o) thuộc y=3x=> y_o=3.x_o

_{\(p=\frac{x_o+1}{3x_o+3}=\frac{x_o+1}{3\left(x_o+1\right)}\)} 

\(\hept{\begin{cases}x_0=-1\Rightarrow P=kXD\\x_o\ne-1\Rightarrow P=\frac{1}{3}\end{cases}}\)