Cho tam giác ABC đều , chứng minh rằng các góc của tam giác đều bằng 60 độ

Những câu hỏi liên quan
chứng minh rằng:
- trong tam giác đều 3 góc bằng nhau và bằng 60 độ
- 1 tam giác có 2 góc bằng nhau và bằng 60 độ là tam giác đều
- tam giác cân có 1 góc bằng 60 độ là tam giác đều
2) góc còn lại là 180 - 2.60=60
vậy 3 góc =60 độ => tam giác đều
Đúng 0
Bình luận (0)
1) 3 góc = nhau => 3*A=180 độ (gọi 3 góc là A,B,C)
=> a=60 độ = góc B = góc C
Đúng 0
Bình luận (0)
giả sử tam giác ABC cân tại A => B=C=60 độ => góc A = 180 -60-60=60=> tam giác đều
với tam giác cân tại B và C thì CMTT
Đúng 0
Bình luận (0)
cho tam giác abc có các góc khác 60 độ và khác 120 độ . về phía ngoài tam giác vẽ các tam giác đều abd và aec gọi m,n,p lần lượt là trung điểm của ad ,ae,bc .chứng minh rằng tam giác mnp là tam giác đều
Cho tam giác ABC cân tại A có góc B bằng \({60^o}\). Chứng minh rằng tam giác ABC đều.
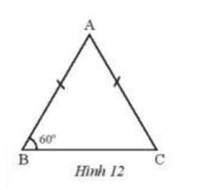
Ta có: tam giác ABC cân tại A
Nên \(\widehat B = \widehat C = {60^o}\)( 2 góc đáy của tam giác cân )
Theo định lí về tổng 3 góc trong tam giác ta có : \(\widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat A = {180^o} - {60^o} - {60^o} = {60^o}\)
Vì \(\widehat A = \widehat B = \widehat C = {60^o}\)\( \Rightarrow \) tam giác ABC là tam giác đều
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A bằng 60 độ. Dựng ra ngoài tam giác đó các tam giác đều ABM và ACN
a) Chứng minh rằng 3 điểm A,M,N thẳng hàng
b) Chứng minh rằng: BN = CM
c) Gọi O là giao điểm của BN và CM. Tính góc BOC
a) Ta có : \(\Delta\) MAB đều => góc MAB = 60 \(^0\)
\(\Delta\)ACN đều => góc CAN = 60 \(^0\)
Ta lại có :góc MAN = \(\widehat{BAC}+\widehat{MAB}+\widehat{CAN}\)=60\(^0\)+60\(^0\)+60\(^0\)
= > 3 điểm A,M,N thẳng hàng (đpcm)
Cho tam giác ABC đều, M là trung điểm của BC, E trên ab, f trên ac sao cho góc MCF bằng 60 độ Chứng minh rằng
a. tam giác EBM đồng dạng tam giác MCF
b. tam giác MBE đồng dạng tam giác EMF\(\)\(\dfrac{StamgiacMEF}{StamgiacABC}\)
Cho tam giác ABC có góc A bằng 60 độ. Vẽ ra phía ngoài của tam giác hai tam giác đều AMB và ANC. Chứng minh rằng 3 điểm M,A,N thẳng hàng và BN = CN.
cho tam giác abc có góc a = 60 độ góc c < góc B < 90 độ
a, cm ab<ac
b cm trên cạnh ac lấy điểm m sao cho am = ab .Chứng minh tam giác abm là tam giác đều
c, so sánh các cạnh của tam giác abc
a: góc C<góc B
=>AB<AC
b: Xét ΔABM co AB=AM và góc A=60 độ
nên ΔAMB đều
Đúng 0
Bình luận (0)
cho tam giác ABC có góc A khác 60 độ . dựng về phía ngoài tam giác ABC 2 tam giác đều ABD và ACE . Lấy AD và CE làm 2 cạnh dựng hình bình hành ADFE . Chứng minh rằng : tam giác FBC là tam giác đều

Gọi M là giao điểm của AE và CF
ADFE là hình bình hành nên ^ADF = ^AEF (hai góc đối)
Suy ra ^BDF = ^FEC
Xét \(\Delta\)BDF và \(\Delta\)FEC có:
BD = FE (cùng bằng AD)
^BDF = ^FEC (cmt)
DF = EC ( cùng bằng AE)
Do đó \(\Delta\)BDF = \(\Delta\)FEC (c.g.c) suy ra BF = CF (1) và ^BFD = ^FCE
Mặt khác ^AMC = ^DFC (do DF // AE)
^AMC = ^MEC + ^FCE = 600 + ^FCE và ^DFC = ^BFC + ^BFD
Do đó ^BFC = 600 (2)
Từ (1) và 2) suy ra \(\Delta\)FBC đều (đpcm)
cho tam giác ABC có góc A = 60 độ. Gọi BE và CF là hai đường cao và M trung điểm của BC. Chứng minh rằng tam giác MFE là tam giác đều.
















