Giai phương trình nghiệm nguyên:x3+2x=2018-y2
Nghiệm của phương trình 2 2 x = 2 x + 2018 là
A. x =2018
B. x = 2018 3
C. x = -2018
D. x = - 2018 3
Nghiệm của phương trình 2 2 x = 2 x + 2018 là
A. x = 2018
B. x = 2018 3
C. x = -2018
D. x = - 2018 3
Nghiệm của phương trình 2 2 x = 2 x + 2018 là.
A. x = 2018
B. x = 2018 3
C. x = - 2018
D. x = - 2018 3
Giải phương trình nghiệm nguyên: x^3+2x=2018-y^2
Số nghiệm nghiệm nguyên nhỏ hơn 2018 của bất phương trình: ( x + 1 ) log 1 2 2 x + ( 2 x + 5 ) log 1 2 x + 6 ≥ 0 là:
A. 2016.
B. 2017.
C. 2018.
D. Vô số.
Đáp án A.
+ Điều kiện: x > 0
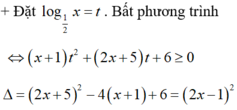
Bất phương trình
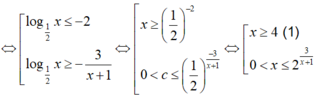
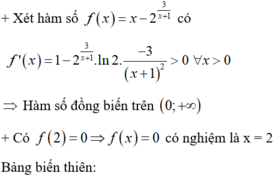
=> Bất phương trình x ≤ 2 3 x + 1 ⇔ f ( x ) ≤ 0 ⇔ 0 < x ≤ 2 ( 2 ) .
Từ (1) và (2) => Tập nghiệm của bất phương trình là
S = ( 0 ; 2 ] ∪ [ 4 ; + ∞ ) .
Vậy có 2016 nghiệm nguyên thỏa mãn.
Số nghiệm nghiệm nguyên nhỏ hơn 2018 của bất phương trình: ( x + 1 ) log 1 2 2 x + ( 2 x + 5 ) log 1 2 x + 6 ≥ 0 là
A. 2016
B. 2017
C. 2018
D. Vô số
Số nghiệm nghiệm nguyên nhỏ hơn 2018 của bất phương trình: ( x + 1 ) log 1 2 2 x + ( 2 x + 5 ) log 1 2 x + 6 ≥ 0 là:
A. 2016
B. 2017
C. 2018
D. Vô số
Đáp án A.
+ Điều kiện: x > 0
+ Đặt log 1 2 x = t . Bất phương trình ⇔ x + 1 t 2 + 2 x + 5 t + 6 ≥ 0
Δ = 2 x + 5 2 − 4 x + 1 + 6 = 2 x − 1 2
Bất phương trình
⇔ log 1 2 x ≤ − 2 log 1 2 x ≥ − 3 x + 1 ⇔ x ≥ 1 2 − 2 0 < c ≤ 1 2 − 3 x + 1 ⇔ x ≥ 4 (1) 0 < x ≤ 2 3 x + 1
+ Xét hàm số f x = x − 2 3 x + 1 có f ' x = 1 − 2 3 x + 1 . ln 2. − 3 x + 1 2 > 0 ∀ x > 0
Hàm số đồng biến trên 0 ; + ∞
+ Có f 2 = 0 ⇒ f x = 0 coa nghiệm là x=2
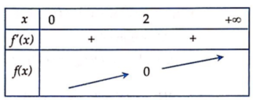
Bảng biến thiên:
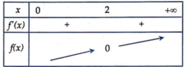
Bất phương trình x ≤ 2 3 x + 1 ⇔ f x ≤ 0 ⇔ 0 < x ≤ 2 ( 2 )
Từ (1) và (2) => Tập nghiệm của bất phương trình là S = 0 ; 2 ∪ 4 ; + ∞
Vậy có 2016 nghiệm nguyên thỏa mãn.
Cho hệ phương trình y 2 - 2 x + 3 = 0 5 x 2 - 7 x y - 6 y 2 = 0 .Giả sử (x;y) là nghiệm của hệ phương trình. Giá trị nhỏ nhất của x 2 + y 2 là:
A. 45
B. 9
C. 2
D. 5
CHo phương trình: x2 - 2x + m = 0
a, Giải phương trình khi m = 7
b, Tìm m để phương trình có nghiệm thỏa mãn x2 + y2 = 5
a) Thay \(m=7\) vào phương trình, ta được:
\(x^2-2x+7=0\)
Xét \(\Delta=\left(-2\right)^2-4.1.7=4-28=-24\)
=> Phương trình vô nghiệm \(\left(\Delta< 0\right)\)
b) Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-\left(-2\right)}{1}=2\\x_1.x_2=\dfrac{m}{1}\end{matrix}\right.\)
Xét \(\Delta=\left(-2\right)^2-4.1.m=4-4m\)
Để phương trình có nghiệm thì \(\Delta\ge0\)
\(\Leftrightarrow4-4m\ge0\\ \Leftrightarrow-4m\ge-4\\ \Leftrightarrow m\le1\)
Theo đề bài, ta có:
\(x^2+y^2=5\\ \Leftrightarrow x^2+y^2+2xy-2xy=5\\ \Leftrightarrow\left(x+y\right)^2-2xy=5\\ \Leftrightarrow2^2-2m=5\\ \Leftrightarrow4-2m=5\\ \Leftrightarrow2m=-1\\ \Leftrightarrow m=-\dfrac{1}{2}\)