Câu 1: Cho đường tròn tâm O bán kính AB=13 cm. Dây CD có độ dài 12cm vuông góc với OA tại H
a) Tính HC,OH
b) Gọi M, N theo thứ tự là hình chiếu của H trên AC,BC. Chứng minh CM.CA=CN.CB
c) Tính diện tích tứ giác CMHN.
Những câu hỏi liên quan
Cho đường tròn tâm O, đường kính AB = 13cm. Dây CD có độ dài bằng 12cm và vuông
góc với AB tại H. Gọi M, N theo thứ tự là hình chiếu của H trên AC, BC. Tính diện tích tứ giác
CMHN.
Cho tam giác ABC nội tiếp đường tròn tâm O. Đường kính AB = 13 cm. Dây CD vuông góc AB tại H và CB = 12 cm. a) Tính các độ dài AC , BC , HA , HB b) Gọi M , N thứ tự là hình chiếu của H trên AC và BC. Chứng minh tứ giác HMCN là hình chữ nhật và tính diện tích tứ giác HMCN
Cho nửa đường tròn tâm O đường kình AB = 13 cm. dây cung CD có độ dài là 12 cm vuông với AB tại H
a) Tính HA ? HB ?
b) Gọi M,N theo thứ tự là hình chiếu của H trên AC, BC. Tính Diện tích của CMHN
a)Ta có:
AO=OB=OD = 13:2=7,5 cm
Theo Py-ta-go suy ra:\(OH=\sqrt{7,5^2-6^2}=4,5cm\)
Do đó:
AH = AO-OH = 7,5-4,5 = 3 cm
HB = OH + OB = 4,5+7,5 = 12 cm
b)Dễ thấy tứ giác CMHN là hcn (do có 3 góc vuông)
Ta có:
+Theo Py-ta-go: \(AC=\sqrt{AH^2+HC^2}=3\sqrt{5}cm\)
+Hệ thức lượng trong tam giác:\(CH^2=CM.AC\)suy ra \(CM=\frac{12\sqrt{5}}{5}cm\)
+Hệ thức lượng trong tam giác:\(\frac{1}{MH^2}=\frac{1}{AH^2}+\frac{1}{CH^2}\)
Suy ra \(MH=\frac{6\sqrt{5}}{5}cm\)
Vậy S(CMHN) = CM.MH = 14,4 CM^2
Đúng 0
Bình luận (0)
3 góc vuông để CNHM là hình chữ nhật là những góc gì vậy ?
Đúng 0
Bình luận (0)
Câu 1: Cho đường tròn tâm O bán kính AB=13 cm. Dây CD có độ dài 12cm vuông góc với OA tại H
a) Tính HC,OH
b) Gọi M, N theo thứ tự là hình chiếu của H trên AC,BC. Chứng minh CM.CA=CN.CB
c) Tính diện tích tứ giác CMHN.
Cho đường tròn (O) đường kính AB 13 cm, dây CD có độ dài 12 cm vuông góc với AB tại Ha, Tính độ dài các đoạn thẳng HA, HBb, Gọi M, N lần lượt là hình chiếu của H trên AC, BC. Tính diện tích tứ giác CMHN
Đọc tiếp
Cho đường tròn (O) đường kính AB = 13 cm, dây CD có độ dài 12 cm vuông góc với AB tại H
a, Tính độ dài các đoạn thẳng HA, HB
b, Gọi M, N lần lượt là hình chiếu của H trên AC, BC. Tính diện tích tứ giác CMHN
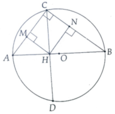
a, Tính được HA=4cm; HB=9cm
b, Tính được HA=4cm; HB=9cm
c, Tính được HM = 12 13 13 cm, HN = 18 13 13 cm
Từ đó tính được S C M H N = 216 13 c m 2
Đúng 1
Bình luận (0)
Câu 1: Cho đường tròn tâm O bán kính AB=13 cm. Dây CD có độ dài 12cm vuông góc với OA tại H
a) Tính HC,OH
b) Gọi M, N theo thứ tự là hình chiếu của H trên AC,BC. Chứng minh CM.CA=CN.CB
c) Tính diện tích tứ giác CMHN.
Câu 1: Cho đường tròn tâm O bán kính AB=13 cm. Dây CD có độ dài 12cm vuông góc với OA tại H
a) Tính HC,OH
b) Gọi M, N theo thứ tự là hình chiếu của H trên AC,BC. Chứng minh CM.CA=CN.CB
c) Tính diện tích tứ giác CMHN.
8.Cho đường tròn tâm O, đường kính AB = 13 cm. Dây CD có độ dài bằng 12 cm vuông góc
với AB tại H.
a) Tính độ dài HB, HA.
b) Gọi M và N lần lượt là hình chiếu của H trên AC, BC. Tính diện tích tứ giác CMHN.
Cho nửa đường tròn tâm O đường kính AB , dây CD có độ dài không đổi và khác AB .
Gọi I là hình chiếu vuông góc của O trên dây CD .
a) Chứng minh I là trung điểm của CD .
b) Gọi H K, theo thứ tự là hình chiếu vuông góc của A B, trên CD . Chứng minh I là trung
điểm của HK .
c) Gọi E là hình chiếu vuông góc của I trên AB . Chứng minh rằng . Diện tích tam giác ACB.diện tích tam giác ADBIO.AB
d*) Tìm vị trí của dây CD để diện tích của tứ giác AHKB là lớn nhất?
Làm ơn giúp mình câu c,d với ạ. Mìn...
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB , dây CD có độ dài không đổi và khác AB . Gọi I là hình chiếu vuông góc của O trên dây CD . a) Chứng minh I là trung điểm của CD . b) Gọi H K, theo thứ tự là hình chiếu vuông góc của A B, trên CD . Chứng minh I là trung điểm của HK . c) Gọi E là hình chiếu vuông góc của I trên AB . Chứng minh rằng . Diện tích tam giác ACB.diện tích tam giác ADB=IO.AB d*) Tìm vị trí của dây CD để diện tích của tứ giác AHKB là lớn nhất? Làm ơn giúp mình câu c,d với ạ. Mình xin chân thành cảm ơn