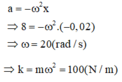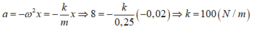Một con lắc lò xo gồm quả cầu m=100(g), lò xo k = 40N/m, dao động điều hòa theo phương nằm ngang trên trục Ox, gốc toạ độ O ở vị trí cân bằng. Biết lúc t = 0 vật có li độ x = +cm và có vận tốc v= +80(cm/s). Phương trình dao động của quả cầu là:

Những câu hỏi liên quan
Một con lắc lò xo gồm lò xo có độ cứng k và vật nhỏ có khối lượng 250 g, dao động điều hòa dọc theo trục Ox nằm ngang (vị trí cân bằng ở O). Ở li độ -2 cm, vật nhỏ có gia tốc 8
m
/
s
2
. Giá trị của k là A. 120 N/m B. 20 N/m C. 100 N/m D. 200 N/m
Đọc tiếp
Một con lắc lò xo gồm lò xo có độ cứng k và vật nhỏ có khối lượng 250 g, dao động điều hòa dọc theo trục Ox nằm ngang (vị trí cân bằng ở O). Ở li độ -2 cm, vật nhỏ có gia tốc 8 m / s 2 . Giá trị của k là
A. 120 N/m
B. 20 N/m
C. 100 N/m
D. 200 N/m
Một con lắc lò xo gồm lò xo có độ cứng k và vật nhỏ có khối lượng 250 g, dao động điều hòa dọc theo trục Ox nằm ngang (vị trí cân bằng ở O). Ở li độ -2cm, vật nhỏ có gia tốc 8 m/s2. Giá trị của k là:
A.120 N/m.
B.200 N/m.
C.20 N/m.
D.100 N/m.
Đáp án D
Phương pháp: Sử dụng công thức tính gia tốc trong dao động điều hòa của con lắc lò xo
Cách giải:
Ta có:
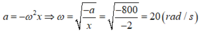
=> Độ cứng k = mω2 = 0,25.202 = 100 N/m
=> Chọn D
Đúng 0
Bình luận (0)
Một con lắc lò xo nằm ngang dao động điều hoà xung quanh vị trí cân bằng với chu kỳ T π/10 s. Đặt trục tọa độ Ox nằm ngang, gốc O tại vị trí cân bằng. Cho rằng lúc t 0, vật ở vị trí có li độ x -1 cm và được truyền vận tốc 20√3 cm/s theo chiều dương. Khi đó phương trình dao động của vật có dạng: A. x 2 sin (20t + π/6) cm. B. x 2 cos (20t - π/6) cm. C. x 2 sin (20t - π/6) cm. D. x 2 sin (20t - π/3) cm.
Đọc tiếp
Một con lắc lò xo nằm ngang dao động điều hoà xung quanh vị trí cân bằng với chu kỳ T = π/10 s. Đặt trục tọa độ Ox nằm ngang, gốc O tại vị trí cân bằng. Cho rằng lúc t = 0, vật ở vị trí có li độ x = -1 cm và được truyền vận tốc 20√3 cm/s theo chiều dương. Khi đó phương trình dao động của vật có dạng:
A. x = 2 sin (20t + π/6) cm.
B. x = 2 cos (20t - π/6) cm.
C. x = 2 sin (20t - π/6) cm.
D. x = 2 sin (20t - π/3) cm.
Chọn C
+ ω = 2π : T = 20 rad/s.
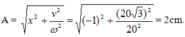
+ t = 0: x = 2cosφ = -1 => 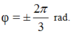
v = -40 sinφ > 0 => sinφ < 0 => ![]()
Vậy: x = 2 cos(20t - 2π/3) = 2 sin(20t - π/6) cm.
Đúng 0
Bình luận (0)
Một con lắc lò xo gồm lò xo có độ cứng k và vật nhỏ có khối lượng 250 g, dao động điều hòa dọc
theo trục Ox nằm ngang (vị trí cân bằng ở O). Ở li độ –2cm, vật nhỏ có gia tốc 8 m/s². Giá trị của k là
Câu này dễ mà bạn, áp dụng CT liên hệ giữa gia tốc với li độ.
\(a=-\omega^2.x\Rightarrow \omega=\sqrt{\dfrac{-a}{x}}=20(rad/s)\)
\(\Rightarrow k=m.\omega^2=0,25.20^2=100(N/m)\)
Đúng 0
Bình luận (0)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() tôi có lần ngủ muộn như vậy nhưng k phải để lên đây, ham vậy
tôi có lần ngủ muộn như vậy nhưng k phải để lên đây, ham vậy![]()
Đúng 0
Bình luận (0)
Một con lắc lò xo gồm lò xo có độ cứng k và vật nhỏ có khối lượng 250g, dao động điều hòa dọc theo trục Ox nằm ngang (vị trí cân bằng ở O). Ở li độ - 2cm, vật nhỏ có gia tốc 8 m / s 2 . Giá trị của k là
A. 20N/m.
B. 120N/m.
C. 200N/m.
D. 100N/m.
Con lắc lò xo gồm vật nhỏ có khối lượng m gắn vào đầu một lò xo nhẹ có độ cứng k đang dao động điều hòa dọc theo trục Ox. Chọn mốc thế năng ở vị trí cân bằng O. Tại một thời điểm, vật có li độ x và vận tốc v. Cơ năng của con lắc lò xo bằng A.
1
2
m
v
2
+
k
x
B.
m
v
2
+
k...
Đọc tiếp
Con lắc lò xo gồm vật nhỏ có khối lượng m gắn vào đầu một lò xo nhẹ có độ cứng k đang dao động điều hòa dọc theo trục Ox. Chọn mốc thế năng ở vị trí cân bằng O. Tại một thời điểm, vật có li độ x và vận tốc v. Cơ năng của con lắc lò xo bằng
A. 1 2 m v 2 + k x
B. m v 2 + k x 2
C. 1 2 m v 2 + k x 2
D. 1 2 m v + k x
Đáp án C
Cơ năng của con lắc lò xo được xác định bởi biểu thức
Đúng 0
Bình luận (0)
Một con lắc lò xo dao động theo trục x nằm ngang. Lò xo có độ cứng 100 N/m ; vật có khối lượng 1,00 kg. Bỏ qua ma sát. Tại t = 0 vật được kéo ra khỏi vị trí cân bằng cho lò xo dãn ra 10 cm rồi thả ra không vận tốc đầu. Chọn gốc toạ độ tại vi trí cân bằng. Viết phương trình dao động.
T = 0,63s ⇒ ω = 10
Tại t = 0 vật ở biên dương nên phương trình dao động của vật là
x = 10cos10t (cm)
Đúng 0
Bình luận (0)
Một con lắc lò xo gồm một vật nhỏ có khối lượng 200 g và một lò xo nhẹ có độ cứng 80 N/m. Con lắc dao động điều hòa theo phương nằm ngang với biên độ 4 cm. Độ lớn vận tốc của vật khi vật ở vị trí cân bằng là
A. 100 cm/s
B. 40 cm/s
C. 80 cm/s
D. 60 cm/s
Một con lắc lò xo nằm ngang gồm quả cầu có khối lượng 100g gắn vào lò xo có khối lượng không đáng kể và có độ cứng k80N/m. Kéo quả cầu ra khỏi vị trí cân bằng theo phương của trục lò xo một đoạn 3cm và đẩy quả cầu về vị trí cân bằng với vận tốc v00,8sqrt{2} m/s. Chọn gốc thời gian là lúc đẩy quả cầu và chiều dương của trục tọa độ ngược chiều vận tốc v0. Viết phương trình dao động của vật.
Đọc tiếp
Một con lắc lò xo nằm ngang gồm quả cầu có khối lượng 100g gắn vào lò xo có khối lượng không đáng kể và có độ cứng k=80N/m. Kéo quả cầu ra khỏi vị trí cân bằng theo phương của trục lò xo một đoạn 3cm và đẩy quả cầu về vị trí cân bằng với vận tốc v0=0,8\(\sqrt{2}\) m/s. Chọn gốc thời gian là lúc đẩy quả cầu và chiều dương của trục tọa độ ngược chiều vận tốc v0. Viết phương trình dao động của vật.
Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)
Đúng 0
Bình luận (0)