Cho ABCD là hình thang vuông tại A;D;AB= 1/3 CD. Kéo dài DA cắt CB tại M
a) So sánh diện tích hai tam giác ABC và ADC
b) So sánh diện tich shai tam giác ABM và ACM
c) Diện tích hình thang ABCD bằng 64 cm2. Tính diện tích tam giác MBA.
Cho hình chóp sabcd có abcd là hình thang vuông tại a,d. Ab=2a, ad=cd=a. Sa=a√2, sa vuông góc abcd a, (sb,(abcd))=? (Sc,(abcd)=? b, kẻ ah vuông góc sc tại h. Ak vuông góc sd tại k (Ah,(sad))=? (Sb,(sac)=?
a.
\(SA\perp\left(ABCD\right)\Rightarrow AB\) là hình chiếu vuông góc của SB lên (ABCD)
\(\Rightarrow\widehat{SBA}=\left(SB;\left(ABCD\right)\right)\)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{SBA}\approx35^016'\)
Tương tự \(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=\left(SC;\left(ABCD\right)\right)\)
\(AC=\sqrt{AD^2+DC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\\AB\perp AD\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
\(\Rightarrow\left(AH;\left(SAD\right)\right)=90^0-\left(AH;AB\right)=90^0-\widehat{HAB}\)
Gọi E là trung điểm AB \(\Rightarrow ADCE\) là hình vuông \(\Rightarrow\widehat{ACE}=45^0\)
Tam giác BCE vuông cân tại E (do \(EB=EC=a\)) nên \(\widehat{ECB}=45^0\)
\(\Rightarrow\widehat{ACB}=90^0\) hay \(BC\perp AC\Rightarrow BC\perp\left(SAC\right)\) (do \(SA\perp BC\))
\(\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp BH\)
Hay tam giác ABH vuông tại H
\(AH=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=a\)
\(\Rightarrow cos\widehat{HAB}=\dfrac{AH}{AB}=\dfrac{1}{2}\Rightarrow\widehat{HAB}=60^0\)
\(\Rightarrow\widehat{HAB}=60^0\Rightarrow\left(AH;\left(SAD\right)\right)=30^0\)
Theo cmt \(BC\perp\left(SAC\right)\Rightarrow\left(SB;\left(SAC\right)\right)=\widehat{BSC}\)
\(SC=\sqrt{SA^2+AC^2}=2a\) ; \(SB=\sqrt{SA^2+AB^2}=a\sqrt{6}\)
\(\Rightarrow cos\widehat{BSC}=\dfrac{SC}{SB}=\dfrac{\sqrt{6}}{3}\Rightarrow\widehat{BSC}\approx35^016'\)
Cho hình thang vuông ABCD vuông góc tại A và D ,AB=1 PHẦN 3 CD . Kéo dài DA và CB cắt nhau tại M . Diện tích hình thang ABCD là 64 cm vuông . tính diện tích tam giác MBA
cho hình thang vuông ABCD vuông tại A .Có đáy DC gấp 2 lần đáy AB .Kéo dài AD cắt BC tại G . Tính diện tích tam giác GAB .Biết diện tích hình thang ABCD là 48 dm2 ?
mình cũng không biết làm bài đó đâu,bạn nào làm đc thì giải giùm đi
Cho hình thang vuông ABCD tại A và D; AD=CD=a; AB=a Quay hình thang ABCD xung quanh đường thẳng CD. Thể tích khối tròn xoay thu được là
A. 5 π a 3 3
B. 7 π a 3 3
C. 4 π a 3 3
D. π a 3
Đáp án A
Gọi V là thể tích của khối tròn xoay cần tính, khi đó V = V 1 − V 2 với
V1 là thể tích khối trụ có chiều cao h 1 = A B , bán kính R = A D → V 1 = π R 2 h 1 = 2 π a 3
V 2 là thể tích khối trụ có chiều cao h 1 = A B − C D , bán kính R = A D → V 2 = 1 3 π r 2 h 2 = π a 3 3
Vậy thể tích cần tính là V = V 1 − V 2 = 2 π a 3 − π a 3 3 = 5 π a 3 3
Cho hình thang ABCD vuông tại A và D, AD=CD=a, AB=2a. Quay hình thang ABCD quanh đường thẳng CD. Thể tích khối tròn xoay thu được là:
![]()
![]()
![]()
![]()
Cho hình thang ABCD vuông tại A và D, A D = C D = a , A B = 2 a . Quay hình thang ABCD quanh đường thẳng CD. Thể tích khối tròn xoay thu được là:
A. 5 πa 3 3
B. 7 πa 3 3
C. 4 πa 3 3
D. πa 3
Chọn đáp án A
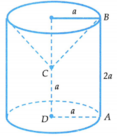
Gọi (T) là khối trụ có đường cao là 2a, bán kính đường tròn đáy là a và (N) là khối nón có đường cao là a, bán kính đường tròn đáy là a
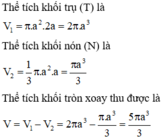
Cho hình thang vuông ABCD , vuông tại A . Có đáy BC gấp 2 lần đáy AB . Kéo dài AD cắt BC tại G . Tính diện tích tam giác GAB . Biết diện tích hình thang ABCD là 48dm2
Cho hình thang vuông ABCD tại A và D, AD = CD = a, AB = 2a. Quay hình thang ABCD xung quanh đường thẳng CD. Thể tích khối tròn xoay thu được là
A. 5 πa 3 3
B. 7 πa 3 3
C. 4 πa 3 3
D. πa 3
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A,B với AB=BC=a , AD=2a , SA vuông góc (ABCD) và SA = a√2 a) Cminh các mặt bên của hình chóp là các tam giác vuông
Cho hình thang ABCD vuông tại A, D. 2 đường chéo vuông góc tại O, AB = 15, AD = 20
a, Tính OB, OD, AC
b, Tính diện tích hình thang ABCD
a: BD=căn 15^2+20^2=25cm
OD=AD^2/BD=400/25=16cm
OB=25-16=9cm
AO=căn 16*9=12cm
ΔADC vuông tại D có DO là đường cao
nên AD^2=AO*AC
=>AC=20^2/12=400/12=100/3(cm)
b: DC=căn AC^2-AD^2=căn (100/3)^2-20^2=80/3cm
S ABCD=1/2*(AB+CD)*AD
=1/2*20*(15+100/3)=10*145/3=1450/3cm2