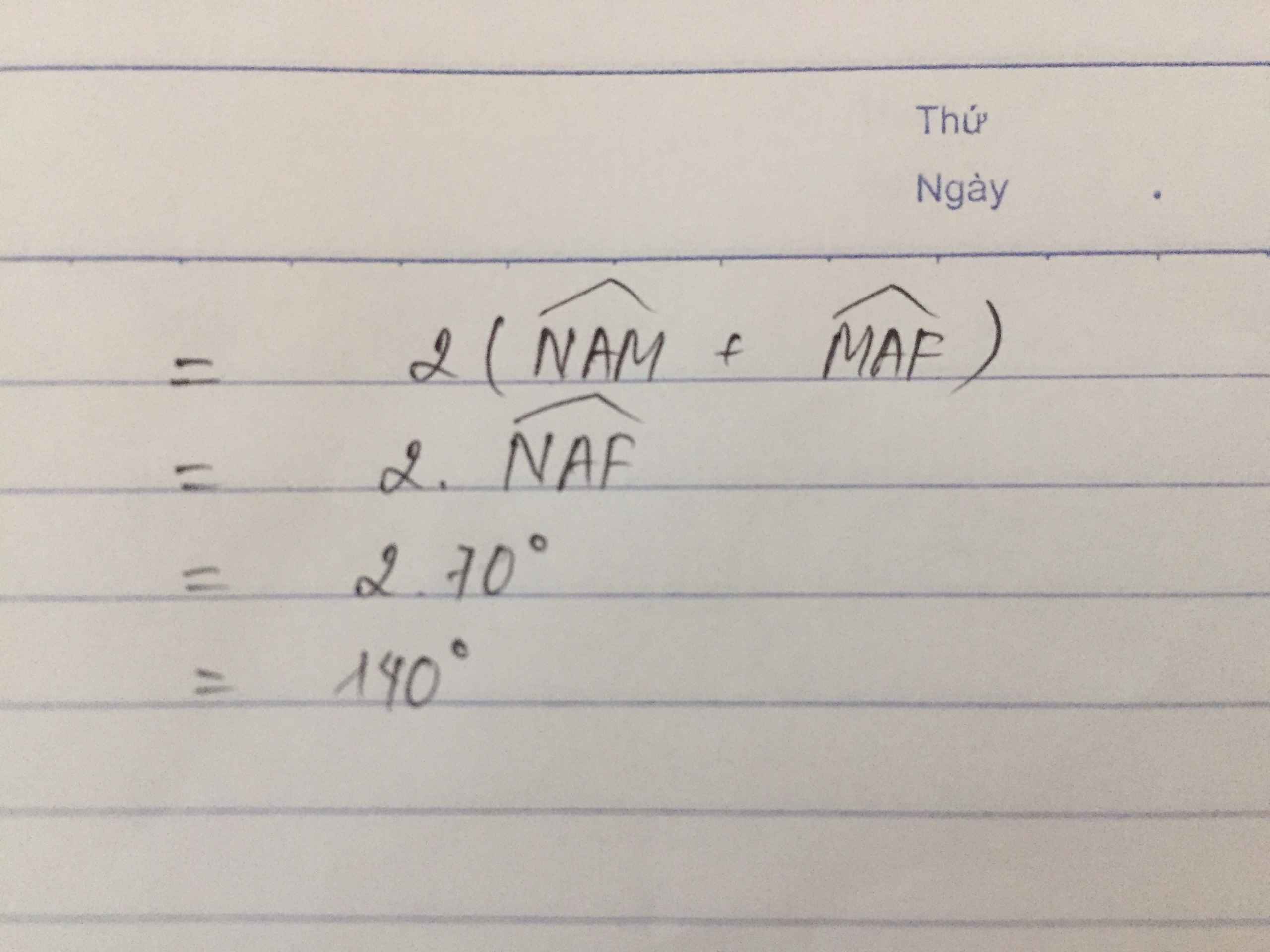Cho tam giác đều ABC cạnh 5cm. Qua A kẻ d // BC. Vẽ D đối xứng của C qua d. Tính CD. (Mấy bạn vẽ hình nha.)

Những câu hỏi liên quan
Cho tam giác đều ABC cạnh 5cm. Qua A kẻ d // BC. Vẽ D đối xứng của C qua d. Tính CD.
Vì ∆ABC đều
=> AB = AC = BC = 5cm
Mà D là điểm đối xứng của C qua d
=> AB = AC = BC = AD = 5cm
Mà DA + AC = 5 + 5 = 10cm
Đúng 0
Bình luận (0)
Cho tam giác ABC đều , cạnh dài 2 cm , đường cao AH .
a) Vẽ D đối xứng vs A qua BC
b) Cm tứ giác ABCD là hình thoi
c) Tính diện tích tam giác ABC
d) Lấy điểm M trên cạnh BD ( M ko trùng B và D ) . Cm ddierm đối xứng của M qua H nằm giữa A và C .
Cho tam giác ABC vuông tại A, AB 5cm, BC 13 cm. Gọi D là trung điểm của AC. Vẽ điểm E đối xứng với điểm B qua D.a) Tính độ dài cạnh AC.b) Chứng minh tứ giác ABCE là hình bình hành. c) Gọi M là điểm đối xứng với B qua A. Tứ giác AMEC là hình gì ? Vì sao?
Đọc tiếp
Cho tam giác ABC vuông tại A, AB = 5cm, BC = 13 cm. Gọi D là trung điểm của AC. Vẽ điểm E đối xứng với điểm B qua D.
a) Tính độ dài cạnh AC.
b) Chứng minh tứ giác ABCE là hình bình hành.
c) Gọi M là điểm đối xứng với B qua A. Tứ giác AMEC là hình gì ? Vì sao?
Hình Tự Vẽ Nhe
a)
Áp dụng định lí PItago vào tam giác ABC ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC^2=BC^2-AB^2=13^2-5^2=12\left(cm\right)\)
b)
Tứ Giác ABCE có:
D là trung điểm của AC (gt)
D là trung điểm của BE ( E đối xứng B qua A )
=> Tứ Giác ABCE là Hình Bình Hành
c)
Ta có:
Vì tứ giác ABCE là hình bình hành => CE=AB; CE//AB ( tính chất hình bình hành ) (1)
Mà M đối xứng với B qua A => AM=AB (2)
CE//AB (cmt) => CE//AM (3)
Từ (1) và (2) (3) => CE//AM và CE=AM
Tứ Giác AMEC có:
CE=AM (cmt)
CE//AM (cmt)
Góc A = 90 độ (gt)
=> Tứ giác AMEC là Hình Chữ Nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A =70 độ, điểm M thuộc cạnh BC vẽ D đối xứng M qua AB, E đối xứng M qua AC
a, CM AD=AE
b, Tính DAE
VẼ HÌNH
Bài 1: *Cho tam giác đều ABC, điểm M thuộc BC. Gọi D là điểm đối xứng với M qua AB, E là điểm đối xứng với M qua AC. Vẽ hình bình hành MDNE. Chứng minh AN song song với BCBài 2:*Cho tam giác ABC. Lấy điểm D,E theo thứ tự thuộc tia đối của các tia BA, CA sao cho BD CE BC. Gọi O là giao điểm của BE & CD. Qua O vẽ đường thẳng song song với tia phân giác của góc A, đường này cắt AC ở K. Chứng ming AB CKMấy bài này mình vô tình lụm được từ mấy cuốn sách cũ năm 1 nghìn chín trăm hồi đó nên không bi...
Đọc tiếp
Bài 1: *Cho tam giác đều ABC, điểm M thuộc BC. Gọi D là điểm đối xứng với M qua AB, E là điểm đối xứng với M qua AC. Vẽ hình bình hành MDNE. Chứng minh AN song song với BC
Bài 2:*Cho tam giác ABC. Lấy điểm D,E theo thứ tự thuộc tia đối của các tia BA, CA sao cho BD = CE = BC. Gọi O là giao điểm của BE & CD. Qua O vẽ đường thẳng song song với tia phân giác của góc A, đường này cắt AC ở K. Chứng ming AB = CK
Mấy bài này mình vô tình lụm được từ mấy cuốn sách cũ năm 1 nghìn chín trăm hồi đó nên không biết là của lớp mấy nha =)) để đại lớp 8 :D
Cho tam giác ABC cân tại A, đường trung tuyến AM. Biết AB5cm, BC6cm. Gọi K là điểm đối xứng với A qua Ma) chứng minh: tứ giác ABKC là hình thoib) Qua A kẻ đường thẳng song song với BC cắt KC kéo dài tại D. Tứ giác ABCD là hình gì? Vì sao?c) Tính số đo góc DAK. Từ đó tính diện tích tam giác DAKd) Tam giác ABC có thêm điều kiện gì thì ABKC là hình vuông?Vẽ hình nữa nha
Đọc tiếp
Cho tam giác ABC cân tại A, đường trung tuyến AM. Biết AB=5cm, BC=6cm. Gọi K là điểm đối xứng với A qua M
a) chứng minh: tứ giác ABKC là hình thoi
b) Qua A kẻ đường thẳng song song với BC cắt KC kéo dài tại D. Tứ giác ABCD là hình gì? Vì sao?
c) Tính số đo góc DAK. Từ đó tính diện tích tam giác DAK
d) Tam giác ABC có thêm điều kiện gì thì ABKC là hình vuông?
Vẽ hình nữa nha
a) Xét \(\Delta\)ABM và \(\Delta\)KCM có: MK = MA ; MB = MC ; ^AMB = ^KMC ( đối đỉnh )
=> \(\Delta\)ABM = \(\Delta\)KCM => AB = KC (1)
Vì \(\Delta\)ABC cân có AM là đường trung tuyến => AM là đường trung trực hay KM là đường trung trực => KB = KC(2)
\(\Delta\)ABC cân => AB = AC (3)
Từ (1) ; (2) (3) => AB = AC = KB = KC => ABKC là hình thoi
b) ABKC là hình thoi => KC //AB => CD //AB mà theo đề AD //BC
=> ABCD là hình bình hành
c) \(\Delta\)ABC cân có AN kaf đường trung tuyến => AM vuông góc BC mà AD // BC => AD vuông AM => ^DAK = ^DAM = 90 độ
Ta có: BM = 1/2 . BC = 6 : 2 = 3 cm AB = 5 cm
\(\Delta\)ABM vuông tại M . Theo định lí Pitago => AM = 4 cm
=> AK = 2AM = 2.4 = 8cm
AD = BC = 6cm ( ABCD là hình bình hành )
=> S ( DAK ) = AD.AK : 2 = 6.8 : 2 = 24 ( cm^2)
d) Để ABKC kaf hình vuông; mà ABKC là hình thoi nên ^BAC = 90 độ
=> tam giác ABC Có thêm điều kiện vuông tại A thì ABKC là hình vuông.
Cho tam giác ABC vuông tại B, D là trung điểm của AC. Qua D kẻ DE//BC(E thuộc AB) và DF//AB (F thuộc BC).
a) Chứng minh tứ giác BEDF là hình chữ nhật
b) Vẽ M đối xứng với D qua E, N đối xứng với D qua F. Chứng minh M,B,N thẳng hàng
c) Tính diện tích tam giác DEF biết diện tích tam giác ABC là 24cm vuông.
a, Ta có: DE//BC \(\Rightarrow\widehat{DEB}+\widehat{EBF}=180\)
mà góc EBF =90 => góc DEB =90 (1)
Chứng minh tương tự với DF//AB
\(\Rightarrow\widehat{EDF}=90;\widehat{BFD}=90\) (2)
Từ (1) và (2) => tứ giác BEDF là hình chữ nhật
Đúng 0
Bình luận (0)
a) vì ED//BC và DF//AB
Mà \(\Delta ABC\)vuông tại B
Nên \(DE\perp AB\)và \(DF\perp BC\)
Xét tứ giác BEDF có:
\(\widehat{B}=\widehat{DEB}=\widehat{DFB}=90^0\)
Vậy tứ giác BEDF là hình chữ nhật
Đúng 0
Bình luận (0)
BÀI 1: Cho tam giác ABC. Trên tia đối của tia BA lấy D, trên tia đối của tia CA lấy E sao cho BD = CE = BC. Gọi M là giao điểm của BE và CD đường thẳng qua M song song với tia phân giác của góc BAC cắt AC ở F. Chứng minh rằng AB = CF.
BÀI 2:Cho tam giác đều ABC, điểm M thuộc cạnh BC. Gọi D là điểm đối xứng với M qua AB, E là điểm đối xứng với M qua AC. Vẽ hình bình hành MDNE. CMR: AN // BC.
“““““` ✬ ‘✧ ‘✬
““““` __♜_♜_♜__
“““` `{,,,,,,,,,,,,,,,,,,,,,}
‘“` ✩`{✫//✰//✰//✫}` ✩
‘“` ♖_{♖___♖__♖___.♖}_♖
“` {///////////////}
“`{,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}
“{//////////////////}
“{_✿__❀_♥_✿_♥_❀__✿_}
““““ * ` ` * ` ` *
‘““““ 0 ` ` 0 ` ` 0
““““ ||___||___||
““ * ` {,,,,,,,,,,,,,,,,,,,} ` *
““ 0 ` {////////} ` 0
‘“`_||_{_______”_____}_||_
“`{///////////////}
“`{,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,}
“`{///////////////}
“`{_____________”________}
Đúng 0
Bình luận (0)
cho abc tia phan giac cua goc b cat ac o d tren tia doi cua tia ba lay e sao cho be = bc chung minh bd song song ec cai nay lam sao
Đúng 0
Bình luận (0)
Cho tam giác đều ABC , điểm M thuộc cạnh BC .Gọi D là điểm đối xứng với M qua AB , E là điểm đối xứng với M qua AC .Vẽ hình bình hành MDNE .Chứng minh rằng AN// BC
O là giao của DE,MN. Từ D,A,O,N,E hạ các đường vuông góc xuống BC và cắt BC tại D',A',O',N',E'.
Đường trung bình: NN′=DD′+EE′(=2OO′)NN′=DD′+EE′(=2OO′)
Q,P là giao của MD,ME với AB,AC →DD′=DQ=MQ,EE′=EP=MP→DD′=DQ=MQ,EE′=EP=MP
Dùng diện tích dễ dàng chứng minh MQ+MP=AA′→AA=DD′+EE′=NN′→AN//BCDPCM
Đúng 0
Bình luận (0)
Xem thêm câu trả lời