Cho hình vẽ AB//CD, ^A=^B.CMR AD=BC ,AC=BD

Những câu hỏi liên quan
Cho hình vẽ biết AB // CD và AD // BC (nó như là hình bình hành ấy, AB và DC là chiều dài)
a) CMR: AB = CD và AD = BC
b) Gọi O là giao điểm của AC và BD, chứng minh O là trung điểm của AC và BD
CHO HÌNH THANG ABCD (AB//CD) CÓ GÓC A LỚN HƠN GÓC B.CMR AC<BD
Ta có góc A>góc B
<=> AC<BD ( cạnh góc đối diện trong tam giác) (đpcm)
Đúng 0
Bình luận (0)
cho hình vẽ là hình thang biết ab// cd và ad// bc. bd cắt ac tại i. cmr: ib=id
Xét tứ giác ABCD có
AB//CD
AD//BC
Do đó: ABCD là hình bình hành
Suy ra: IB=ID
Đúng 0
Bình luận (0)
cho hình thang cân ABCD ( AB//CD ) , AB = BC và BC vuông góc với BD vẽ giúp mình hình với
chứng min AC vuông góc với AD
Vì ABCD là hình thang cân nên \(AD=BC,\widehat{ADC}=\widehat{BCD}\)
Xét 2 tam giác ADC và BCD có: DC chung, \(\widehat{ADC}=\widehat{BCD}\), AD=BC
\(\Rightarrow\Delta ADC=\Delta BCD\left(c.g.c\right)\Rightarrow\widehat{DAC}=\widehat{CBD}=90^0\Rightarrow AC\perp AD\)
Cho bốn điểm A, B, C, D tạo thành hình có AB / / CD và BC//AD như hình vẽ. Giao điểm của AC và BD là O. Từ O vẽ vuông góc với AC cắt cạnh BC, AD lần lượt tại M, N. Chứng minh AC là trung trực của MN và AM = MC = CN = NA
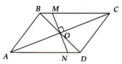
cho hình vẽ biết AB song song với CD ; AD song song với BC.
a, chứng minh AB =CD; AD = BC
b,gọi O là giao điểm của AC và BD . Chứng minh O là chung điểm của AC và BD
c,gọi M, N lần lượt là trung điểm của BC và CD ;gọi E,F lần lượt là giao điểm của BD với AM và AN. chứng minh BE=EF=FD
a. Do AB//CD nên góc ABD = BDC, ADB = CBD. Suy ra \(\Delta ABD=\Delta CDB\left(g-c-g\right)\Rightarrow AB=CD,AD=BC\)
b. Dễ thấy \(\Delta AOB=\Delta COD\left(g-c-g\right)\Rightarrow OA=OC,OB=OD\)
c. Xét tam giác ABC có AM và BO là các đường trung tuyến nên E là trọng tâm, vậy OB = 2EO.
Tương tự DF=2FO. Mà OD = OB. Vậy BE = EF = DF.
Đúng 0
Bình luận (0)
Cho hình thang ABCD có AB//CD và AB<CD. Qua A vẽ đường thẳng AK//BC (K thuộc CD). Qua B vẽ đường thẳng BI//AD (I thuộc CD) ; BI cắt AC ở F, AK cắt BD ở E.
Chứng minh rằng:
a) EF//AB
b) AB^2=CD.EF
Câu 8: Trong hình vẽ bên các cặp cạnh song song với nhau là: (0,5 điểm) A. AH và HC ;AB và AHB. AB và BC ; CD và AD C. AB và DC;Ad và BCD. AB và CD; AC và BD
Đọc tiếp
Câu 8: Trong hình vẽ bên các cặp cạnh song song với nhau là: (0,5 điểm)
A. AH và HC ;AB và AH
B. AB và BC ; CD và AD
C. AB và DC;Ad và BC
D. AB và CD; AC và BD
Xem thêm câu trả lời
Cho hình thang ABCD (ab//cd) O là giao điểm của 2 đường chéo AC và BD . ĐUowngf thẳng vẽ qua O // AD cắt AD và BC theo thứ tự tại M và N . CMR : 1/AB + 1/CD = 2/MN
Sửa đề: Đường thẳng qua O song song với AB
Xét ΔAOB và ΔCOD có
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
\(\widehat{BAO}=\widehat{DCO}\)(hai góc so le trong, AB//CD)
Do đó: ΔAOB\(\sim\)ΔCOD(g-g)
Suy ra: \(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)(Các cặp cạnh tương ứng tỉ lệ)
\(\Leftrightarrow\dfrac{OA}{OB}=\dfrac{OC}{OD}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{OA}{OB}=\dfrac{OC}{OD}=\dfrac{OA+OC}{OB+OD}=\dfrac{AC}{BD}\)
\(\Leftrightarrow\dfrac{OC}{OD}=\dfrac{AC}{BD}\)
\(\Leftrightarrow\dfrac{CO}{CA}=\dfrac{DO}{DB}\)(1)
Xét ΔDAB có
M∈AD(gt)
O∈BD(gt)
MO//AB(gt)
Do đó:\(\dfrac{DO}{DB}=\dfrac{MO}{AB}\)(Hệ quả của Định lí Ta lét)(2)
Xét ΔABC có
O∈AC(gt)
N∈BC(gt)
ON//AB(gt)
Do đó: \(\dfrac{CO}{CA}=\dfrac{ON}{AB}\)(Hệ quả của Định lí Ta lét)(3)
Từ (1), (2) và (3) suy ra \(\dfrac{OM}{AB}=\dfrac{ON}{AB}\)
hay OM=ON(đpcm)
\(\Leftrightarrow OM+ON=MN=2\cdot ON\)
Xét ΔBCD có
O∈BD(gt)
N∈BC(gt)
ON//DC(gt)
Do đó: \(\dfrac{ON}{CD}=\dfrac{BN}{BC}\)(Hệ quả của Định lí Ta lét)(4)
Xét ΔABC có
O∈AC(gt)
N∈BC(gt)
ON//DC(gt)
Do đó: \(\dfrac{ON}{AB}=\dfrac{CN}{CB}\)(Hệ quả của Định lí Ta lét)
\(\Leftrightarrow\dfrac{ON}{AB}+\dfrac{ON}{CD}=\dfrac{BN}{BC}+\dfrac{CN}{BC}=1\)
\(\Leftrightarrow\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{1}{ON}=\dfrac{2}{2\cdot ON}=\dfrac{2}{MN}\)(đpcm)
Đúng 1
Bình luận (0)





















