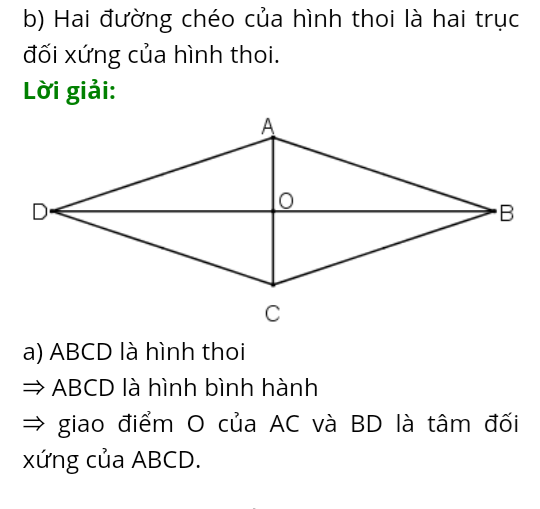
chứng minh rằng trong hình thoi giao điểm 2 đường chéo là tâm đối xứng của hình thoi

Những câu hỏi liên quan
Chứng minh rằng : a, Giao điểm 2 đường chéo của hình thoi là tâm đối xứng của hình thoi b, Hai đường chéo của hình thoi là 2 trục đối xứng của hình thoi
Chứng minh rằng:
a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi.
b) Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi.
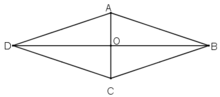
a) ABCD là hình thoi
⇒ ABCD là hình bình hành
⇒ giao điểm O của AC và BD là tâm đối xứng của ABCD.
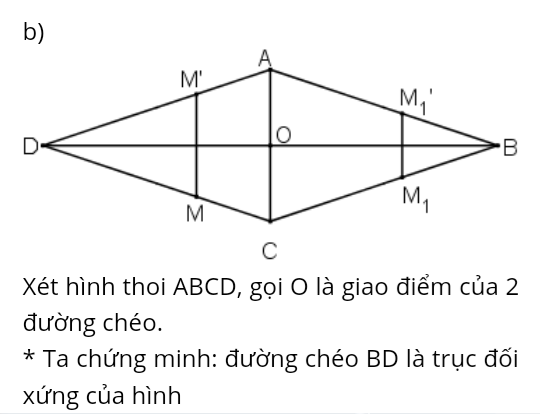
b)
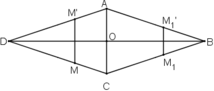
ét hình thoi ABCD, gọi O là giao điểm của 2 đường chéo.
* Ta chứng minh: đường chéo BD là trục đối xứng của hình
Lấy điểm M bất kì thuộc hình thoi. Không mất tổng quát, M nằm trên CD.
Gọi M’ đối xứng với M qua đường thẳng BD. Ta chứng minh điểm M’ cũng thuộc hình thoi
+ Gọi I là giao điểm của MM’ và BD.
Xét tam giác DIM và DIM’ có:
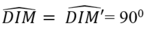
DI chung
IM= IM’ ( do M và M’ đối xứng với nhau qua BD)
=> ∆ DIM = ∆ DIM’ ( c.g.c)
=> DM = DM’ và 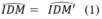
Lại có: ABCD là hình thoi nên
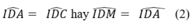
Từ (1) và (2) suy ra, điểm M’ nằm trên cạnh AD hay điểm M’ thuộc hình thoi
=> BD là trục đối xứng của hình thoi.
*Chứng minh tương tự, ta có: AC là trục đối xứng của hình thoi.
Đúng 0
Bình luận (0)
chứng minh rằng trong hình thoi
a) giao điểm hai đường chéo là tâm đối xứng của hình thoi
b) hai đường chéo là hai trục đối xứng của hình thoi
a,
ABCD là hình thoi
=> ABCD là hình bình hành
=> Giao điểm O của AC và BD là tâm đối xứng của ABCD.
Xét hình thoi ABCD, gọi O là giao điểm của 2 đường chéo.
* Ta chứng minh: đường chéo BD là trục đối xứng của hình
Lấy điểm M bất kì thuộc hình thoi. Không mất tổng quát, M nằm trên CD.
Gọi M’ đối xứng với M qua đường thẳng BD. Ta chứng minh điểm M’ cũng thuộc hình thoi
+ Gọi I là giao điểm của MM’ và BD.
Xét tam giác DIM và DIM’ có :
\(\widehat{DIM}=\widehat{DIM'}=90^o\)
DI chung
IM= IM’ ( do M và M’ đối xứng với nhau qua BD)
\(\Rightarrow\Delta DIM=\Delta DIM'\left(c-g-c\right)\left(1\right)\)
Lại có: ABCD là hình thoi nên
\(\widehat{IDA}=\widehat{IDC}\)và \(\widehat{IDM}=\widehat{IDA}\left(2\right)\)
Từ (1) và (2) suy ra, điểm M’ nằm trên cạnh AD hay điểm M’ thuộc hình thoi
=> BD là trục đối xứng của hình thoi.
*Chứng minh tương tự, ta có: AC là trục đối xứng của hình thoi.
Chứng minh rằng
a) Giao điểm 2 đường chéo của hình thoi là tâm đối xứng của hình thoi
b) 2 đường chéo của hình thoi là 2 trục đối xứng của hình thoi
a)
a) ABCD là hình thoi
=> ABCD là hình bình hành
=> giao điểm O của AC và BD là tâm đối xứng của ABCD
b)
Xét hình thoi ABCD, gọi O là giao điểm của 2 đường chéo.
* Ta chứng minh: đường chéo BD là trục đối xứng của hình
Lấy điểm M bất kì thuộc hình thoi. Không mất tổng quát, M nằm trên CD.
Gọi M’ đối xứng với M qua đường thẳng BD. Ta chứng minh điểm M’ cũng thuộc hình thoi
+ Gọi I là giao điểm của MM’ và BD.
Xét tam giác DIM và DIM’ có :
\(\widehat{DIM}=\widehat{DIM'}=90^o\)
DI chung
IM= IM’ ( do M và M’ đối xứng với nhau qua BD)
\(=>\Delta DIM=\Delta DIM'\left(c.g.c\right)\)
=> DM = DM' và \(\widehat{IDM}=\widehat{IDM'}\left(1\right)\)
Ta lại có: ABCD là hình thoi nên
\(\widehat{IDA}=\widehat{IDC}\)hay \(\widehat{IDM}=\widehat{IDA}\left(2\right)\)
Từ (1) và (2) suy ra, điểm M’ nằm trên cạnh AD hay điểm M’ thuộc hình thoi
=> BD là trục đối xứng của hình thoi.
*Chứng minh tương tự, ta có: AC là trục đối xứng của hình thoi
Chứng minh rằng trong hình thoi: Giao điểm của hai đường thẳng chéo là tâm đối xứng của hình thoi.
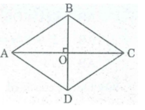
Hình bình hành có tâm đối xứng là giao điểm của hai đường chéo. Hình thoi cũng là một hình bình hành nên cũng có tâm đối xứng là giao điểm hai đường chéo của nó.
Đúng 0
Bình luận (0)
Chứng minh rằng:
-giao điểm hai đường chéo hình thoi là tâm đối xứng của hình thoi
-hai đường chéo của hình thoi là hai trục đối xứng của hình thoi
a) Ta có hình thoi đồng thời là HBH
=> 2 đường chéo căt nhau tại trung điểm mỗi đường
=> 2 đường chéo của hình thoi đối xứng vs nhau
b) Từ câu a
=> 2 đường chéo đó cũng là trục đối xứng
Đúng 0
Bình luận (0)
a) Ta có hình thoi đồng thời là HBH
=> 2 đường chéo căt nhau tại trung điểm mỗi đường
=> 2 đường chéo của hình thoi đối xứng vs nhau
b) Từ câu a => 2 đường chéo đó cũng là trục đối xứng
Đúng 0
Bình luận (0)
- Hình bình hành nhận giao điểm hai đường chéo là tâm đối xứng. Hình thoi cũng là một hình bình hành nên giao điểm hai đường chéo hình thoi là tâm đối xứng của hình.
- BD là đường trung trực của AC (do BA = BC, DA = DC) nên A đối xứng với C qua BD.
B và D cũng đối xứng với chính nó qua BD.
Do đó BD là trục đối xứng với chính nó qua BD.
Do đó BD là trục đối xứng của hình thoi.
Tương tự AC cũng là trục đối xứng của hình thoi.
Đúng 0
Bình luận (0)
Chứng minh rằng :
a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi
b) Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi
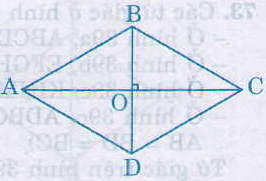
a) Hình bình hành nhận giao điểm hai đường chéo là tâm đối xứng. Hình thoi cũng là một hình bình hành nên giao điểm hai đường chéo hình thoi là tâm đối xứng của hình.
b) BD là đường trung trực của AC (do BA = BC, DA = DC) nên A đối xứng với C qua BD.
B và D cũng đối xứng với chính nó qua BD.
Do đó BD là trục đối xứng với chính nó qua BD.
Do đó BD là trục đối xứng của hình thoi.
Tương tự AC cũng là trục đối xứng của hình thoi.
Đúng 0
Bình luận (0)
Bài giải:

a) Hình bình hành nhận giao điểm hai đường chéo là tâm đối xứng. Hình thoi cũng là một hình bình hành nên giao điểm hai đường chéo hình thoi là tâm đối xứng của hình.
b) BD là đường trung trực của AC (do BA = BC, DA = DC) nên A đối xứng với C qua BD.
B và D cũng đối xứng với chính nó qua BD.
Do đó BD là trục đối xứng với chính nó qua BD.
Do đó BD là trục đối xứng của hình thoi.
Tương tự AC cũng là trục đối xứng của hình thoi.
Đúng 0
Bình luận (0)
Bài giải:

a) Hình bình hành nhận giao điểm hai đường chéo là tâm đối xứng. Hình thoi cũng là một hình bình hành nên giao điểm hai đường chéo hình thoi là tâm đối xứng của hình.
b) BD là đường trung trực của AC (do BA = BC, DA = DC) nên A đối xứng với C qua BD.
B và D cũng đối xứng với chính nó qua BD.
Do đó BD là trục đối xứng với chính nó qua BD.
Do đó BD là trục đối xứng của hình thoi.
Tương tự AC cũng là trục đối xứng của hình thoi.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng:
a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi.
b) Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi.
a) Hình bình hành nhận giao điểm hai đường chéo là tâm đối xứng. Hình thoi cũng là một hình bình hành nên giao điểm hai đường chéo hình thoi là tâm đối xứng của hình.
b) BD là đường trung trực của AC (do BA = BC, DA = DC) nên A đối xứng với C qua BD.
B và D cũng đối xứng với chính nó qua BD.
Do đó BD là trục đối xứng với chính nó qua BD.
Do đó BD là trục đối xứng của hình thoi.
Tương tự AC cũng là trục đối xứng của hình thoi.
Đúng 0
Bình luận (0)
Cô ơi cô vẽ hình và chỉ rõ giúp em ở câu a) là tâm đối xứng là điểm nào nhe cô và cô giải thích trong hình này vì sao vì sao 2 đường chéo này đáp ứng đủ những yếu tố gì để kết luận chúng là tâm đối xứng nhe cô. Cô ơi còn ở câu b) thì cô chỉ giúp em trục đối xứng là chỗ nào nhe cô và cô giải thích giúp em trong hình này vì sao vì sao 2 đường chéo này đáp ứng đủ những yếu tố gì để kết luận chúng là trục nhe cô, em cám ơn cô nhìu ạ. hihiChứng minh rằng :a) Giao điểm 2 đường chéo của hình thoi chính...
Đọc tiếp
Cô ơi cô vẽ hình và chỉ rõ giúp em ở câu a) là tâm đối xứng là điểm nào nhe cô và cô giải thích trong hình này vì sao vì sao 2 đường chéo này đáp ứng đủ những yếu tố gì để kết luận chúng là tâm đối xứng nhe cô. Cô ơi còn ở câu b) thì cô chỉ giúp em trục đối xứng là chỗ nào nhe cô và cô giải thích giúp em trong hình này vì sao vì sao 2 đường chéo này đáp ứng đủ những yếu tố gì để kết luận chúng là trục nhe cô, em cám ơn cô nhìu ạ. hihi
Chứng minh rằng :
a) Giao điểm 2 đường chéo của hình thoi chính là tâm đối xứng của hình thoi
b) Hai đường chéo của hình thoi là 2 trục đối xứng của hình thoi