a) Ta có:

IA = IB = IC

Tam giác BAC có AI là trung tuyến và AI = BC/2

⇒ Tam giác BAC vuông tại A hay ∠BAC = 90 0

giúp mình vs

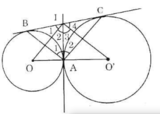
Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC.

tam giác ABC có đường trung tuyến AI = 1/2 BC nên là tam giác vuông

vậy  B A C ^ = 90 o

b) Ta có: 

Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên:

O I O ' ^ = O I A ^ + O ' I A ^ = 1 2 A I B ^ + 1 2 A I C ^ = 1 2 A I B ^ + A I C ^

Vậy O I O ' ^ = 90 o

a: Xét (O) có

ID,IA là các tiếp tuyến

Do đó: IO là phân giác của góc DIA

=>\(\widehat{DIA}=2\cdot\widehat{OIA}\)

Xét (O') có

IA,IE là các tiếp tuyến

Do đó: IO' là phân giác của góc AIE

=>\(\widehat{AIE}=2\cdot\widehat{AIO'}\)

Ta có: \(\widehat{DIA}+\widehat{EIA}=180^0\)(hai góc kề bù)

=>\(2\left(\widehat{OIA}+\widehat{O'IA}\right)=180^0\)

=>\(2\cdot\widehat{OIO'}=180^0\)

=>\(\widehat{OIO'}=90^0\)

b: Xét (O) có

ID,IA là các tiếp tuyến

Do đó: ID=IA

Xét (O') có

IA,IE là các tiếp tuyến

Do đó: IA=IE

Ta có: IA=IE

ID=IA

Do đó: ID=IE

=>I là trung điểm của DE

=>I là tâm đường tròn đường kính DE

Xét ΔDAE có

AI là bán kính

\(AI=\dfrac{DE}{2}\)

Do đó: ΔADE vuông tại A

=>A nằm trên (I)

Xét (I) có

IA là bán kính

O'O\(\perp\)IA tại A

Do đó: OO' là tiếp tuyến của (I)

=>O'O là tiếp tuyến của đường tròn đường kính DE

ΔOIO' vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:

    IA2 = AO.AO' = 9.4 = 36

=> IA = 6 (cm)

Vậy BC = 2.IA = 2.6 = 12 (cm)

c) Xét tam giác OIO' vuông tại I, IA là đường cao có:

IA 2  = O'A.OA = 4.9 = 36 ⇒ IA = 6 cm

Lại có: BC = 2 AI ⇒ BC = 12 (cm)