Cho tam giác ABC vuông tại A có I là. Trung điểm của AC . Trên tia đối của tia IB lấy điểm D sao cho IB =ID
a)cm AB//CD
b)cho biết góc CID=60o. Tính góc CDI
c) gọi H là điểm nằm giữa B,C. HI cắt AD tại K. Cm AK=CH
Những câu hỏi liên quan
Chp tam giác ABC vuông tạo A có I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D sao cho IB = ID.
a) cm AB//CD
b) Cho biết góc CID =60o. tính góc CDI
C) Gọi H là điểm nằm giữa B và C,HI cắt AD tại K. Cm AK=CH
Bài 1 :Cho ABC nhọn (AB AC). Gọi M là trung điểm của BC. Trên tia AM lấy đi ểm N sao cho M là trung điểm của AN.a/. Ch/m : ΔAMB ΔNMCb/. Vẽ CD bot AB (Din AB). So sánh góc ABC và góc BCN. Tính góc DCN.c/. Vẽ AH bot BC (H in BC), trên tia đối của tia HA lấy điểm I sao cho HI HA.Ch/m : BI CN.BÀI 2 :Vẽ góc nhọn xAy. Trên tia Ax lấy hai điểm B và C (B nằm giữa A và C). Trên tia Ay lấy hai điểm D và E sao cho AD AB; AE ACa) Chứng minh BE DCb) Gọi O là giao điểm BE và DC. Chứng minh tam giác OBC...
Đọc tiếp
Bài 1 :
Cho ABC nhọn (AB < AC). Gọi M là trung điểm của BC. Trên tia AM lấy đi ểm N sao cho M là trung điểm của AN.
a/. Ch/m : ΔAMB = ΔNMC
b/. Vẽ CD \bot AB (D\in AB). So sánh góc ABC và góc BCN. Tính góc DCN.
c/. Vẽ AH \bot BC (H \in BC), trên tia đối của tia HA lấy điểm I sao cho HI = HA.
Ch/m : BI = CN.
BÀI 2 :
Vẽ góc nhọn xAy. Trên tia Ax lấy hai điểm B và C (B nằm giữa A và C). Trên tia Ay lấy hai điểm D và E sao cho AD = AB; AE = AC
a) Chứng minh BE = DC
b) Gọi O là giao điểm BE và DC. Chứng minh tam giác OBC bằng tam giác ODE.
c) Vẽ trung điểm M của CE. Chứng minh AM là đường trung trực của CE.
Bài 3
Cho tam giác ABC ( AB< AC ) . Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D, sao cho IB = ID. Chứng minh :
a) Tam giác AIB bằng tam giác CID.
b) AD = BC v à AD // BC.
Bài 4.
Cho tam giác ABC ( AB< AC ) . Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D, sao cho IB = ID. Chứng minh :
a) Tam giác AIB bằng tam giác CID.
b) AD = BC v à AD // BC.
Bài 4.
Cho tam giác ABC ( AB< AC ) . Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D, sao cho IB = ID. Chứng minh :
a) Tam giác AIB bằng tam giác CID.
b) AD = BC v à AD // BC.
BÀI 4
Cho tam giác ABC có góc A =350 . Đường thẳng AH vuông góc với BC tại H. Trên đường vuông góc với BC tại B lấy điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho AH = BD.
a) Chứng minh ΔAHB = ΔDBH.
b) Chứng minh AB//HD.
c) Gọi O là giao điểm của AD và BC. Chứng minh O là trung điểm của BH.
d) Tính góc ACB , biết góc BDH= 350 .
Bài 5 :
Cho tam giác ABC cân tại A và có \widehat{A}=50^0 .
Tính \widehat{B} và \widehat{C}
Lấy D thuộc AB, E thuộc AC sao cho AD = AE. Chứng minh : DE // BC.
Bài 6 :
Cho tam giác ABC cân tại A. Lấy D thuộc AC, E thuộc AB sao cho AD = AE.
Chứng minh : DB = EC.
Gọi O là giao điểm của BD và EC. Chứng minh : tam giác OBC và ODE là tam giác cân.
Chứng minh rằng : DE // BC.
Bài 7
Cho tam giác ABC. Tia phân giác của góc C cắt AB tại D. trên tia đối của tia CA lấy điểm E sao cho CE = CB.
Chứng minh : CD // EB.
Tia phân giác của góc E cắt CD tại F. vẽ CK vuông góc EF tại K. chứng minh : CK Tia phân giác của góc ECF.
Bài 8 :
Cho tam giác ABC vuông tại A có \widehat{B}=60^0 . Vẽ Cx vuông góc BC, trên tia Cx lấy điểm E sao cho CE = CA (CE , CA nằm cùng phía đối BC). trên tia đối của tia BC lấy điểm F sao cho BF = BA. Chứng minh :
Tam giác ACE đều.
A, E, F thẳng hàng.
Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có ABC=60. Gọi I là trung điểm của AC, trên tia đối của ta IB lấy điểm D sao cho ID=IB.
a) Tính số đo góc ACB
b) Chứng minh : tam giác AIB= tâm giác CID từ đó suy ra CD vuông góc AC và CD//AB
c) CM : tam giác IBC = tam giác IDA từ đó suy ra AD//BC
d) Đường thẳng qua C song song với DB cắt tia AB tại K
Chứng Minh : tam giác ABD = tam giác BKC
các bạn tự vẽ hình nha
a) góc acb là : b+c=90 (hai góc phụ nhau)
c=90-60
c=30
b) xét tam giác aib và tam giác cid ta có
Đúng 0
Bình luận (0)
tiếp theo là có AI =IC (GT) GÓC AIB=GÓC DIC (HAI GÓC ĐỐI ĐỈNH) BI=DI DO ĐÓ TAM GIÁC AIB =TAM GIÁC CID (C-G-C) C) XÉT TAM GIÁC IDA VÀ TAM GIÁC IBC TA CÓ
IB=ID(GT) GÓC AIC=GÓC CIB(HAI GÓC ĐỐI ĐỈNH) AI=IC(GT) DO ĐÓ HAI TAM GIÁC BẰNG NHAU THEO TRƯỜNG HỢP C-G-C
Đúng 0
Bình luận (0)
cho tam giác ABC(AB<AC).Gọi I là trung điểm AC,Trên tia đối của tia IB lấy D sao cho IB=ID
a)chứng minh:ABCD là hình bình hành
b)Gọi H,K lần lượt là trung điểm IB,ID,Chứng minh:AK=HC
c)AH cắt BC tại M;CK cắt AD tại N.Chứng minh:M,I,N thẳng hàng
a: Xét tứ giác ABCD có
I là trung điểm của đường chéo AC
I là trung điểm của đường chéo BD
Do đó: ABCD là hình bình hành
b: Xét tứ giác AKCH có
I là trung điểm của đường chéo AC
I là trung điểm của đường chéo KH
Do đó: AKCH là hình bình hành
Suy ra: AK=HC
Đúng 0
Bình luận (0)
cho tam giác ABC(AB<AC).Gọi I là trung điểm AC,Trên tia đối của tia IB lấy D sao cho IB=ID
a)chứng minh:ABCD là hình bình hành
b)Gọi H,K lần lượt là trung điểm IB,ID,Chứng minh:AK=HC
c)AH cắt BC tại M;CK cắt AD tại N.Chứng minh:M,I,N thẳng hàng
Cho tam giác ABC có góc A lớn hơn 90độ. Gọi I là trung điểm của cạnh AC. Trên tia đối của tia IB lấy điểm D sao cho IBIDa/CM: tam giác AIBtám giác CIDb/CM:ADBCc/Gọi M trung điểm của BC, N trung điểm của AD. CM: I trung điểm của MNd/CM: Góc AIB bé hơn góc BICe/Tìm điều kiện tam giác ABC để AC vuông góc CDPS:làm nhanh giúp mình với mình cần rất rất gấp
Đọc tiếp
Cho tam giác ABC có góc A lớn hơn 90độ. Gọi I là trung điểm của cạnh AC. Trên tia đối của tia IB lấy điểm D sao cho IB=ID
a/CM: tam giác AIB=tám giác CID
b/CM:AD=BC
c/Gọi M trung điểm của BC, N trung điểm của AD.
CM: I trung điểm của MN
d/CM: Góc AIB bé hơn góc BIC
e/Tìm điều kiện tam giác ABC để AC vuông góc CD
PS:làm nhanh giúp mình với mình cần rất rất gấp
a.Xét tam giác AIBAIB và tam giác CIDCID có:
IA=ICIA=IC ( gt )
Góc CIDCID = Góc AIBAIB (ĐỐI ĐỈNH)
ID=IBID=IB ( gt )
⇒Tam giác AIBAIB = Tam giác CIDCID
b.Ta có Tam giác ABIABI = tam giác CDICDI
nên khoảng cách trung tuyến của MIMI và NINI đều bằng nhau.
⇒ II là trung điểm của đoạn MN.MN.
c.Xét góc AIBAIB và góc BICBIC ta có:
IA<ICIA<IC ( gt )
Góc BICBIC > Góc AIBAIB
IC>IBIC>IB ( gt )
⇒Góc AIBAIB < góc BICBIC
d.Điều kiện : Góc AA = 90o
Đúng 0
Bình luận (1)
a, Xét tam giác AIB và tam giác CID có:
AI=CI (gt)
BI=DI(gt)
gócBIA=gócCID (đối đỉnh)
=>tam giác AIB=tam giác CID(c.g.c)
b, Xét tam giác BIC và tam giác DIA có:
BI=DI(gt)
AI=IC(gt)
góc BIC=gócDIA(đối đỉnh)
=>tam giác BIC= tam giác DIA(c.g.c)
=>AD=BC(2 cạnh tương ứng)
c, Do tam giác BIC=tam giác DIA( câu b)
=> góc BCI=góc DAI (2 góc tương ứng)
Do BC=AD(câu b)
=> MC=AN ( đều là trung điểm của BC và AN)
Xét tam giác AIN và tam giác CIM có:
AI=IC (gt)
AN=MC(cm trên)
góc DAI=góc BCI (cm trên)
=>tam giác AIN=tam giác CIM(c.g.c)
=>IM=IN ( 2 cạnh tương ứng)
=> góc AIN= góc CIM ( 2 góc tương ứng)
Mà góc ÂIN+ góc NIC=180 độ ( 2 góc kề bù)
Do 3 điểm A,I,c thẳng hàng
=> góc CIM+NIC=180 độ ( vì góc AIN=CIM)
=> 3 điểm M,I,N thẳng hàng(1)
MI=NI ( câu c) (2)
từ (1) và (2) suy ra I là trung điểm của MN
d, Xét tam giác AIB có BIC là góc ngoài của tam giác AIB
=> góc BIC >Â>90 độ
=> góc BIC>90 độ
=> góc BIC > góc AIB
hay góc AIB<BIC
e,Xét tam giác ABI và tam giác CDI có:
AI=CI (gt)
góc BIA= góc CID (đối đỉnh)
BI=DI ( gt)
=> góc BAI=DCI ( 2 góc tương ứng)
nên để AC vuông góc CD hay DCI=90 độ thì BAI=90 độ
hay tam giác AIB vuông ở A.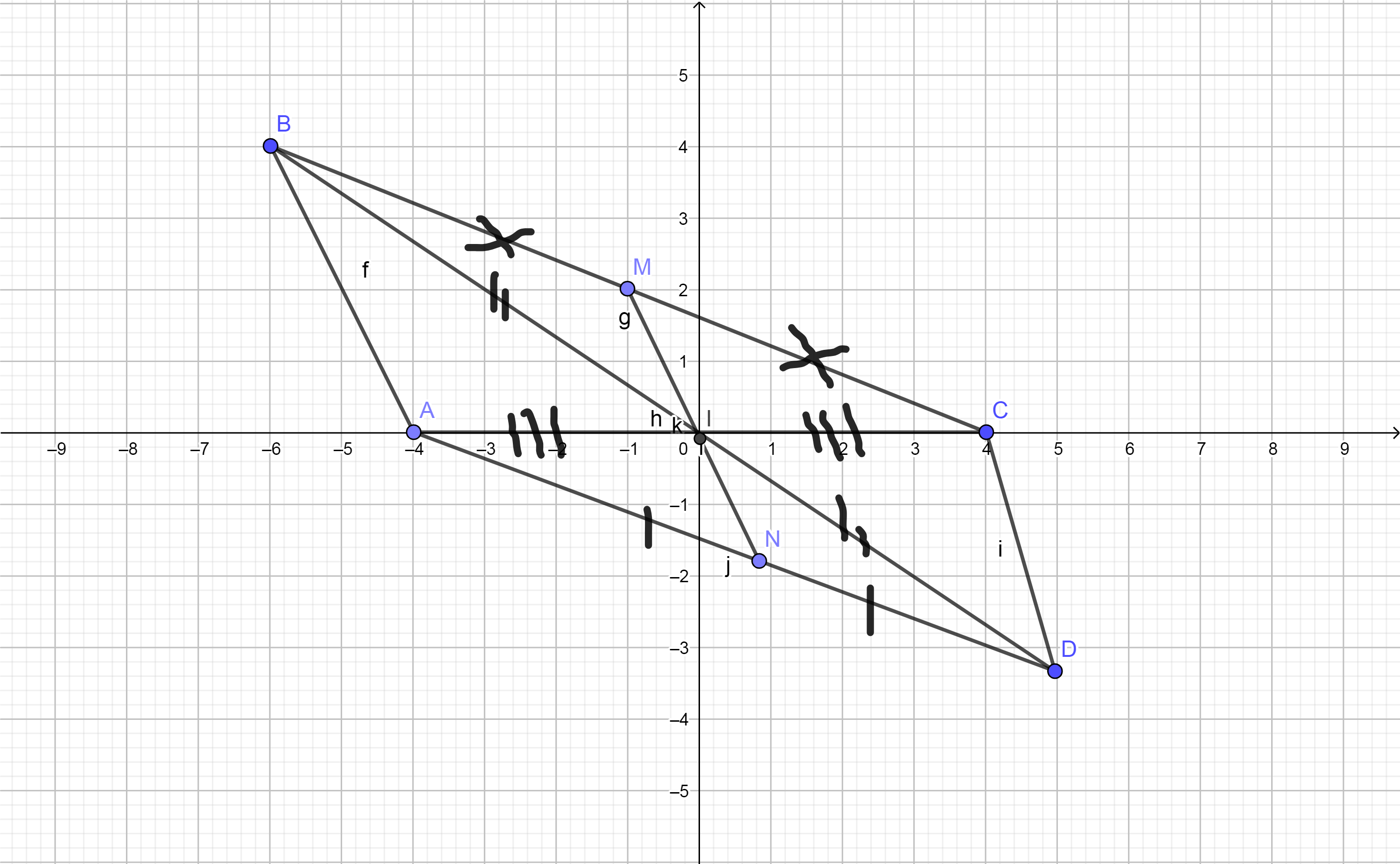
Đúng 0
Bình luận (0)
🙄😀😁😂🤣😃😄😅😆
Cho tam giác ABC vuông tại A có AB= 9cm, BC= 15cm.
a) Tính AC
b) Gọi I là trung điểm của AC. Trên tia đối của tia IB, lấy điểm D sao cho ID=IB. CM tam giác IAD= tam giác ICB
c) Gọi H và K lần lượt là trung điểm của BC và AD. CM I là trung điểm của HK
d) BK và AC cắt nhau tại G. Tính độ dài GB
Cho tam giác ABC ( AB< AC ). Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D, sao cho IB = ID. Chứng minh : a) Δ AIB = Δ CID. b) AD = BC và AD // BC. c) Gọi E là trung điểm của AB. Trên tia đối của tia EC lấy điểm K sao cho: EC = EK. Chứng minh: D, A, K thẳng hàng.
a) Xét Δ AIB và Δ CID:
+ IB = ID (gt).
+ IA = IC (I là trung điểm của AC).
+ ^AIB = ^CID (2 góc đối đỉnh).
=> Δ AIB = Δ CID (c - g - c).
b) Xét tứ giác ABCD có:
+ I là trung điểm của AC (gt).
+ I là trung điểm của BC (IB = ID).
=> Tứ giác ABCD là hình bình hành (dhnb).
=> AD = BC và AD // BC (Tính chất hình bình hành).
c) Xét tứ giác KABC có:
+ E là trung điểm của AB (gt).
+ E là trung điểm của KC (EC = EK).
=> Tứ giác KABC là hình bình hành (dhnb).
=> KA // BC (Tính chất hình bình hành).
Mà AD // BC (cmt).
=> 3 điểm D, A, K thẳng hàng (đpcm).
Đúng 1
Bình luận (0)
Bài 12: Cho tam giác ABC có AB AC. Trên tia đối của tia CA lấy điểm D sao cho CD AB. Gọi H, K lần lượt là trung điểm của AD, BC. Trung trực AD, BC cắt nhau tại I. Vẽ IE vuông góc với AB tại E.a) Chứng minh : IB IC; IA ID.b) Chứng minh: và AI là phân giác của góc BAC.c) Chứng minh: BE HC và AI là đường trung trực của đoạn thẳng EH.d) Từ C kẻ đường thẳng song song với AB, cắt đường thẳng EH tại F. Chứng minh: và E, K, F thẳng hàng.
Đọc tiếp
Bài 12: Cho tam giác ABC có AB < AC. Trên tia đối của tia CA lấy điểm D sao cho CD = AB. Gọi H, K lần lượt là trung điểm của AD, BC. Trung trực AD, BC cắt nhau tại I. Vẽ IE vuông góc với AB tại E.
a) Chứng minh : IB = IC; IA = ID.
b) Chứng minh: và AI là phân giác của góc BAC.
c) Chứng minh: BE = HC và AI là đường trung trực của đoạn thẳng EH.
d) Từ C kẻ đường thẳng song song với AB, cắt đường thẳng EH tại F. Chứng minh: và E, K, F thẳng hàng.