bó tay

chúng cơm chúng à

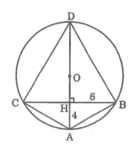
Kéo dài đường cao AH cắt đường tròn ngoại tiếp tam giác ABC tại D . Gọi O là tâm đường tròn ngoại tiếp tam giác ABC 

Vì tam giác ABC cân tại A nên AHlà đường trung trực của BC . Nên  AD là đường trung trực của BC . 

Khi đó O thuộc AD hay AD là đường kính của đường tròn ngoại tiếp tam giác ABC 

Tam giác ACD nội tiếp trong (O )  có AD là đường khính suy ra \(\widehat{ACD=90}\)độ 

Tam giác ACD vuông tại C nên theo hệ thức liên hệ giữa đường cao và hình chiếu , ta có :

\(CH^2=HA.HD\)

\(\Rightarrow\)\(HD=\frac{CH^2}{HA}=\frac{\left(\frac{BC}{2}\right)^2}{HA}=\frac{\left(\frac{12}{2}^2\right)}{4}=\frac{6^2}{4}=9cm\)

Ta có \(AD=AH+HD=4+9=13\left(cm\right)\)

Vậy bán kính của đường tròn (O )  là :

 \(R=\frac{AD}{2}=\frac{13}{2}=6,5\left(cm\right)\)

Chúc bạn học tốt !!!

(Hình)

Diện tích tam giác ABC là:

S_ABC = 1/2 . AH . BC = 1/2 . 4 . 12 = 24 (cm²)

Vì tam giác ABC cân tại A nên đường cao AH là trung tuyến BC

Nên : BH= HC= 1/2. BC= 1/2 . 12 = 6 (cm)

Trong tam giác AHB:

Áp dụng ĐL pi-ta-go:

 AB² = AH² + BH²

AB² = 4² + 6²

AB= \(2\sqrt{13}\) (cm)

Vì tam giác ABC cân tại A nên : AB = AC = \(2\sqrt{13}\) (cm)

Ta có : S_ABC =\(\frac{AB\cdot AC\cdot BC}{4R}\)   (R là bán kính đường tòn ngoại tiếp tam giác ABC)

<=> \(24=\frac{2\sqrt{13}.2\sqrt{13}.12}{4R}\)

<=> R= \(\frac{13}{2}\) (cm)

OK

Chuẩn rồi đấy

Kéo dài đường cao AH cắt đường tròn ngoại tiếp tam giác ABC tại D. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC.

Vì tam giác ABC cân tại A nên AH là đường trung trực của BC. Suy ra AD là đường trung trực của BC.

Khi đó O thuộc AD hay AD là đường kính của đường tròn ngoại tiếp tam giác ABC.

Tam giác ACD nội tiếp trong (O) có AD là đường kính nên suy ra góc (ACD) = 90 °

Tam giác ACD vuông tại C nên theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: C H 2  = HA.HD

Sửa lại giúp mình là BC=12cm