1,cho góc xOy khác góc bẹt.Điểm C chuyển động trên tia Ox,điểm D chuyển động trên tia Oy sao cho OC+OD=a.Các trung điểm M của DC nằm trên đường thẳng nào?

Những câu hỏi liên quan
1,cho góc xOy khác góc bẹt.Điểm C chuyển động trên tia Ox,điểm D chuyển động trên tia Oy sao cho OC+OD=a.Các trung điểm M của DC nằm trên đường thẳng nào?
Cho góc xOy cố định, điểm A cố định trên tia Ox, điểm B cố định trên tia Oy, C di động trên tia Ox, D di động trên tia Oy sao cho OA=OB; OC=OD. I la giao điểm của AD và BC. Hỏi điểm I di động trên đường nào ?
Cho góc vuông xOy, điểm A cố định trên tia Oy, điểm B di động trên tia Ox. Trên tia AB lấy điểm C sao cho B là trung điểm của đoạn thẳng AB. Hỏi C chuyển động trên đường nào ?
Vẽ CQ vuông góc đường thẳng OA tại Q.
mà OB vuông góc OA (vì góc xOy vuông)
\(\Rightarrow OB\) song song CQ
\(\Delta ACQ\)có B là trung điểm AC
OB song song CQ (cmt)
\(\Rightarrow\)O là trung điểm AQ hay Q đối xứng A qua O
* VẬY bất kỳ vị trí của điểm B trên tia Ox thì điểm C luôn di chuyển trên đường thẳng đối xứng với A qua O và vuông góc với OA
Đúng 0
Bình luận (0)
Cho góc XOY vuông, điểm A cố định trên tia Oy, điểm B chuyển động trên tia Ox.vẽ tam giác đều ABC(C và O nằm khác phía đối vs A, B).Khi điểm B chuyển động trên tia Ox thì điểm C chuyển động trên đường nào
Cho góc xOy cố định khác góc bẹt. Các điểm A và B theo thứ tự chuyển động trên các tia Ox và Oy sao cho OA = OB. Đường vuông góc với OB tại B cắt nhau ở M. Điểm M chuyển động trên đường nào ?
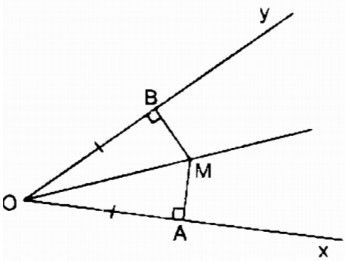
Xét hai tam giác vuông MOA và MOB:
\(\widehat{MAO}=\widehat{MBO}=90^0\)
OA = OB (gt)
OM cạnh huyền chung
Do đó: ∆ MAO = ∆ MBO (cạnh huyền, cạnh góc vuông)
⇒\(\widehat{AOM}=\widehat{BOM}\)
A và B thay đổi, OA và OB luôn bằng nhau nên ∆ MAO và ∆ MBO luôn luôn bằng nhau do đó \(\widehat{AOM}=\widehat{BOM}\)
Vậy khi A chuyển động trên Ox, B chuyển động trên Oy mà OA = OB thì điểm M chuyển động trên tia phân giác của góc xOy.
Đúng 0
Bình luận (0)
cho góc xOy<180 độ các điểm A,B chuyển động trên tia Ox,Oy sao cho OA+OB=4cm M là trung điểm AB. M chuyển đọng trên đường nào
Cho góc xOy cố định khác góc bẹt. Các điểm A và B theo thứ tự chuyển động trên các tia Ox và Oy sao cho OA = OB. Đường vuông góc với OA tại A và đường vuông góc với OB tại B cắt nhau ở M. Điểm M chuyển động trên đường nào ?
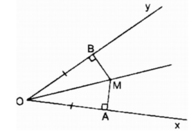
Xét hai tam giác vuông MOA và MOB: ∠ (MAO) = ∠ (MBO) = 90 0
OA = OB (gt)
OM cạnh huyền chung
Do đó: ∆ MAO = ∆ MBO (cạnh huyền, cạnh góc vuông)
⇒ ∠ (AOM) = ∠ (BOM)
A và B thay đổi, OA và OB luôn bằng nhau nên ∆ MAO và ∆ MBO luôn luôn bằng nhau do đó ∠ (AOM) = ∠ (BOM)
Vậy khi A chuyển động trên Ox, B chuyển động trên Oy mà OA = OB thì điểm M chuyển động trên tia phân giác của góc xOy.
Đúng 0
Bình luận (0)
Cho góc xOy khác góc bẹt.a) Từ điểm M trên tia phân giác của góc xOy, kẻ các đường vuông góc MA, MB đến hai cạnh Ox, Oy (A thuộc Ox, B thuộc Oy), OM cắt AB tại H. Chứng minh
A
B
⊥
O
M
.
b) Trên tia đối của tia Ox, Oy lần lượt lấy hai điểm C và D, sao cho OC OD. Hai đương thẳng lần lượt vuông góc với Ox, Oy tại C và D cắt nhau ở E. Chứng minh ba điểm O, H, E thẳng hàng.
Đọc tiếp
Cho góc xOy khác góc bẹt.
a) Từ điểm M trên tia phân giác của góc xOy, kẻ các đường vuông góc MA, MB đến hai cạnh Ox, Oy (A thuộc Ox, B thuộc Oy), OM cắt AB tại H. Chứng minh A B ⊥ O M .
b) Trên tia đối của tia Ox, Oy lần lượt lấy hai điểm C và D, sao cho OC = OD. Hai đương thẳng lần lượt vuông góc với Ox, Oy tại C và D cắt nhau ở E. Chứng minh ba điểm O, H, E thẳng hàng.
Cho góc XOY vuông, điểm A cố định trên tia Oy, điểm B chuyển động trên tia Ox.vẽ tam giác đều ABC(C và O nằm khác phía đối vs A, B).Khi điểm B chuyển động trên tia Ox thì điểm C chuyển động trên đường nào
ai có Vip thì hỏi cô Loan zúp mk đc ko mjk cảm ơn nhìu













