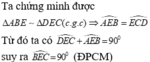Hình thangABCD, AB=6cm, CD=12cm, AD=10cm, E thuộc AD sao cho AE=8cm .Chứng minh BE vuông góc với EC

Những câu hỏi liên quan
Cho hình thang vuông ABCD tại A và D, AB = 6cm, CD = 12cm, AD = 17cm. Trên cạnh AD, lấy E sao cho AE = 8cm. Chứng minh B E C ^ = 90 0 .
Cho hình thang vuông ABCD ( ∠ A = ∠ D = 90 0 ) AB = 6cm, CD = 12cm, AD = 17cm. Trên cạnh AD, đặt đoạn AE = 8cm. Chứng minh ∠ (BEC) = 90 0
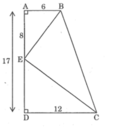
Ta có: AD = AE + DE
Suy ra: DE = AD – AE = 17 – 8 = 9cm
Xét △ ABE và △ DEC, ta có:
∠ A = ∠ D = 90 0 (1)
Mà :
Suy ra: 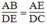 (2)
(2)
Từ (1) và (2) suy ra : △ ABE đồng dạng △ DEC (c.g.c)
Suy ra: ∠ ABE = ∠ DEC
Trong △ ABE ta có: ∠ A = 90 0 ⇒ ∠ (AEB) + ∠ (ABE) = 90 0
Suy ra: ∠ (AEB) + ∠ (DEC) = 90 0
Lại có: ∠ (AEB) + ∠ (BEC) + ∠ (DEC) = 180 0 (kề bù)
Vậy : ∠ (BEC) = 180 0 - ( ∠ (AEB) + ∠ (DEC)) = 180 0 - 90 0 = 90 0
Đúng 2
Bình luận (0)
1. Cho tam giác ABC vuông tại A. Dựng AD vuông góc BC tại D. Đường phân giác CE cắt AD tại F. Chứng minhfrac{FD}{FA}frac{EA}{EB}2. Cho tam giác ABC vuông tại A, AC8cm, BC20cm. Đường trung trực của BC cắt đường thẳng AC tại D, cắt BC tại I. Tính CD.3. Cho hình thang vuông ABCD (góc Agóc D90 độ), AB6cm,CD12cm, AD17cm. Trên cạnh AD đặt đoạn thẳng AE8cm. Chứng minh EB vuông góc EC.
Đọc tiếp
1. Cho tam giác ABC vuông tại A. Dựng AD vuông góc BC tại D. Đường phân giác CE cắt AD tại F. Chứng minh\(\frac{FD}{FA}=\frac{EA}{EB}\)
2. Cho tam giác ABC vuông tại A, AC=8cm, BC=20cm. Đường trung trực của BC cắt đường thẳng AC tại D, cắt BC tại I. Tính CD.
3. Cho hình thang vuông ABCD (góc A=góc D=90 độ), AB=6cm,CD=12cm, AD=17cm. Trên cạnh AD đặt đoạn thẳng AE=8cm. Chứng minh EB vuông góc EC.
Cho hình thang ABCD ( AB//CD ; AB < CD ) . Trên CD lấy E sao cho DE = AB .
. a , chứng minh ABED là hình bình hành
. b , Gọi M là trung điểm của DC , I là trung điểm của AE . IM cắt AB tại N . Chứng minh MN = BC
. c , AB = 10cm ; AC = 6cm ; BC = 8cm ; CD = 15 cm . Chứng minh AD vuông góc với BC
. Mình cần gấp ahihi
.
a)Xét hình bình hành ABED có:
AB=DE
AB//DE(doAB//DC)
=>tứ giác ABED là hình bình hàXetnh vì có 2 cạnh đối // và = nhau(dấu hiệu nhận biết thứ 3)
b)Có AB//DE=>gócBAE=góc AED(2 góc so le trong )
Xét tam giác ANI và tam giác EMI có:
AI=IE(là trung điểm AI)
góc BAE=gócAED(cmt)
góc AIN=gócEIM(2 góc đối đỉnh)
=>tam giác ANI=tam giác EIM(g.c.g)
=>AN=ME(2 cạnh tương ứng)
có AB=DE
AN=ME
=>AB-AN=DE-ME
=>NB=DM
mà DM=MC(do M là trung điểm DC)
=>NB=MC
Lại có NB//MC (do AB//DC)
Xét tứ giác NBMC có :
NB=MC(cmt)
NB//MC(cmt)
=>tứ giác NBMC là hình bình hành vì có 2 cạnh đối //và= nhau(dhnb thứ 3)
=>NM=BC
c)
Đúng 0
Bình luận (0)
a , Vì E \(\in\)CD =) DE // AB .
. Xét tứ giác ABED có DE// AB ; AB=DE =) ABED là hình bình hành
. -
.
.
.
. Xét tứ giác ABED có DE// AB ; AB=DE =) ABED là hình bình hành
. -
.
.
.
Đúng 0
Bình luận (0)
Đoạn xét tam giác sai nha bạn , không cần chứng minh góc BAE = AED vì nó không thuộc tam giác . Thay vì đó xét góc NAI = MEI thì đúng hơn .
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD, tại A và D, AD = 6cm, CD = 12 cm và AD =17 cm. Trên cạnh AD lấy điểm E sao cho AE = 8cm. Chứng minh góc BEC = 90 độ
Đây nha bn !!
nha
Cho ∆ABC vuông tại A có BC=15cm, BA= 8cm.
a) Tính Ác
b) Trên BC lấy E sao cho BA=BE. Kẻ BH vuông góc với AE tại H. Chứng minh HA=HE
c) Trên tia đối tia AB lấy D sao cho AD=EC. Chứng minh AC=DE
d) BH vuông góc với DC
Mình cần gấp
Xem chi tiết
Bạn nên ktra lại con số 15cm
a/ Áp dụng định lí Pythagoras cho t/g ABC vuông tại A có
\(AB^2+AC^2=BC^2\)
=> \(AC=\sqrt{161}\) (cm)
b/ t/g ABH vuông tại H và t/g EBH vuông tại H có
AB = EB
BH : chung
=> t/g ABH=t/g EBH (ch-cgv)
=> HA = HE (2 cạnh t/ứ)
c/ Có \(\widehat{BAH}=\widehat{BEH}\) (do t/g ABH = t/g EBH)
=> \(180^o-\widehat{BAH}=180^o-\widehat{BEH}\)
=> \(\widehat{EAD}=\widehat{AEC}\)
=> t/g AEC = t/g EAD
=> AC = DE
d/
AB = BEAD = EC
=> AB + AD = BE + EC
=> BD = BC=> t/g BCD cân tại B
Có t/g ABH = t/g EBH
=> \(\widehat{ABH}=\widehat{EBH}\)
=> BH là pg góc ABEHay BH là pg góc DBCXét t/g BDC có BH là đường pg
=> BH đồng thời là đường cao
=> BH ⊥ DC
Đúng 2
Bình luận (0)
cho hình thang ABCD vuông ở B , cạnh AD=6cm , BC=12cm,AB=8cm,trên cạnh DC lấy điểm E sao cho BE chia hình thang thành hai phần có diện tích bằng nhau.tính tỉ số BE trên EC?
Xem chi tiết
cho hình thang ABCD vuông ở B , cạnh AD=6cm , BC=12cm,AB=8cm,trên cạnh DC lấy điểm E sao cho BE chia hình thang thành hai phần có diện tích bằng nhau.tính tỉ số BE trên EC?
Xem chi tiết
Cho ΔABC cân tại A (Å < 90 độ). Vẽ BE vuông góc với AC tại E, CD vuông góc với AB tại D.
a/ Chứng minh BE = CD
b/ Cho BC = 10cm, BD = 6cm. Tính CD
c/ Chứng minh AD = AE
d/ Gọi I là giao điểm của BE và CD. Chứng minh ΔBIC cân
e/ Chứng minh AI là tia phân giáp của góc BAC
a: Xét ΔABE vuông tại E và ΔACD vuông tại D có
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACD
b: \(CD=\sqrt{10^2-6^2}=8\left(cm\right)\)
c: Ta có: ΔABE=ΔACD
nên AE=AD
d: Xét ΔDBC vuông tại D và ΔECB vuông tại E có
BC chung
DC=BE
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
hay ΔBIC cân tại I
Đúng 0
Bình luận (0)