a) Xét ΔDAN,ΔHANΔDAN,ΔHAN có :

HN=ND(gt)HN=ND(gt)

ANDˆ=ANHˆ(=90O)AND^=ANH^(=90O)

AN:ChungAN:Chung

=> ΔDAN=ΔHAN(c.g.c)ΔDAN=ΔHAN(c.g.c)

b) Xét ΔAMH,ΔAMEΔAMH,ΔAME có :

HM=ME(gt)HM=ME(gt)

AMHˆ=AMEˆ(=90o)AMH^=AME^(=90o)

AM:ChungAM:Chung

=> ΔAMH=ΔAME(c.g.c)ΔAMH=ΔAME(c.g.c)

Xét tứ giác ANHM có :

Nˆ=90O(HN⊥AB)N^=90O(HN⊥AB)

Aˆ=90O(ΔABC⊥A)A^=90O(ΔABC⊥A)

Mˆ=90O(HM⊥AC)M^=90O(HM⊥AC)

=> Tứ giác ANHM là hình chữ nhật

=> {NH=AMNA=HM{NH=AMNA=HM (tính chất hình chữ nhật)

Ta dễ dàng chứng minh được : ΔANH=ΔAMH(c.c.c)ΔANH=ΔAMH(c.c.c)

Mà : {ΔAND=ΔANHΔAHM=ΔAEM(cmt){ΔAND=ΔANHΔAHM=ΔAEM(cmt)

Suy ra : ΔAND=ΔAMEΔAND=ΔAME

=> DA=AEDA=AE(2 cạnh tương ứng) (*)

c) Từ (*) => A là trung điểm của DE

Do đó : D,A,E thẳng hàng (đpcm)

a: Xét tứ giác AMHN có

\(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)

Do đó: AMHN là hình chữ nhật

b: Xét ΔABC có

H là trung điểm của BC

HN//AB

Do đó: N là trung điểm của AC

Xét ΔABC có

H là trung điểm của BC

HM//AC

Do đó: M là trung điểm của AB

Xét tứ giác AHBP có

M là trung điểm chung của AB và HP

=>AHBP là hình bình hành

Hình bình hành AHBP có AB\(\perp\)HP

nên AHBP là hình thoi

Để AHBP là hình vuông thì \(\widehat{HBP}=90^0\)

AHBP là hình thoi nên BA là phân giác của góc HBP

=>\(\widehat{HBA}=\dfrac{1}{2}\cdot\widehat{HBP}=45^0\)

=>\(\widehat{ABC}=45^0\)

a: Xét ΔAHD có 

AN là đường cao

AN là đường trung tuyến

Do đó:ΔAHD cân tại A

mà AB là đường trung tuyến

nên AB là tia phân giác của góc HAD(1)

Xét ΔAHE có 

AM là đường cao

AM là đường trung tuyến

Do đó: ΔAHE cân tại A

mà AC là đường cao

nên AC là tia phân giác của góc HAE(2)

Từ (1) và (2) suy ra \(\widehat{DAE}=2\cdot\left(\widehat{BAH}+\widehat{CAH}\right)=2\cdot90^0=180^0\)

hay D,A,E thẳng hàng

b: Xét ΔHED có

M là trung điểm của HE

N là trung điểm của HD

Do đó: MN là đường trung bình

=>MN//ED

d: Xét ΔDHE có 

HA là đường trung tuyến

HA=DE/2

Do đó:ΔDHE vuông tại H

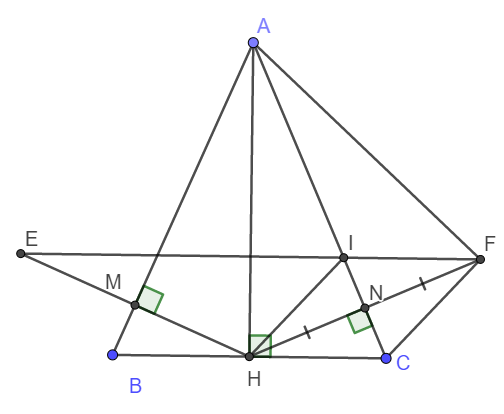
a) Do ABC là tam giác cân tại A nên AH là đường cao hay đồng thời là đường phân giác.

Xét tam giác vuông AMH và tam giác vuông ANH có:

Cạnh AH chung

\(\widehat{MAH}=\widehat{NAH}\)

\(\Rightarrow\Delta AMH=\Delta ANH\)  (Cạnh huyền - góc nhọn)

\(\Rightarrow HM=HN.\)

b) Dễ dàng thấy ngay AC là đường trung trực của HF.

Khi đó thì AH = AF; CH = CF

Xét tam giác AHC và tam giác AFC có:

Cạnh AC chung

AH - AF

CH = CF

\(\Rightarrow\Delta AHC=\Delta AFC\left(c-c-c\right)\)

\(\Rightarrow\widehat{AFC}=\widehat{AHC}=90^o\Rightarrow AF\perp CF.\)

c) Ta thấy ngay \(\Delta HIN=\Delta FCN\left(g-c-g\right)\)

\(\Rightarrow IN=CN\)

Xét tam giác vuông INF và tam giác vuông CNH có:

HN = FN

IN = CN

\(\Rightarrow\Delta INF=\Delta CNH\)  (Hai cạnh góc vuông)

\(\Rightarrow\widehat{IFN}=\widehat{CHN}\)

Mà chúng lại ở vị trí so le trong nên IF // BC.

d) Chứng minh tương tự câu c, ta có IE // BC

Vậy thì qua I có hai tia IE và IF cùng song song với BC nên chúng trùng nhau.

Vậy I, E, F thẳng hàng.

moi hok lop 6