Cho (O) và hai dây AB và CD (AB>CD) cắt tại M ở ngoài (O). Vẽ (O; OM). Gọi F, G là giao điểm với MA, MC và (O; OM)
a) So sánh MF và MG
b) So sánh góc MOF và MOG
Những câu hỏi liên quan
Từ A ngoài ( O ) vẽ hai tiếp tuyến AB và AC với ( O ). Qua C vẽ dây CE song song với AB, AE cắt ( O ) tại D. Tia CD cắt AB tại K
Cho đường tròn (O) có dây cung AB và CD với AB > CD. Giao điểm K của các đường thẳng AB và CD nằm ngoài (O). Vẽ đường tròn (O; OK), đường tròn này cắt KA và KC lần lượt tại M và N. Chứng minh KM < KN
Cho đường tròn tâm O bán kính R, hai dây cung AB và CD, các tia BA và DC cắt nhau tại M nằm ngoài (O) a) Biết AB=CD chứng minh MA=MC. b) Nếu AB>CD, hãy so sánh khoảng cách từ điểm M đến trung điểm của các dây AB, CD
Từ điểm E ở ngoài đường tròn (O) vẽ hai tiếp tuyến tại A và B với đường tròn. Gọi M là điểm thuộc AB; vẽ dây CD sao cho M là trung điểm của CD. Hai tiếp tuyến với đường tròn tại C và D cắt nhau tại F. Cmr tam giác OEF vuông.
22 tháng 9 2021 lúc 9:37
Cho đường tròn tâm O, hai dây AB > CD. AB cắt CD tại điểm M nằm ngoài đường tròn (O) (A nằm giữa M và B; C nằm giữa M và D). Gọi H, K lần lượt là trung điểm AB, CD.
Chứng minh MH > MK
Cho đường tròn (O), dây AB và dây CD, AB < CD. Giao điểm K của các đường thẳng AB, CD nằm ngoài đường tròn. Đường tròn (O; OK) cắt KA và KC tại M và N. Chứng minh rằng KM < KN.
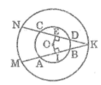
Kẻ OI ⊥ AB, OE ⊥ CD
Trong (O; OA) ta có: AB < CD (gt)
Suy ra : OI > OE (dây lớn hơn gần tâm hơn)
Trong (O ; OK) ta có : OI > OE (cmt)
Suy ra : KM < KN (dây gần tâm hơn thì lớn hơn)
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính R, hai dây cung AB và CD, các tia BA và DC cắt nhau tại M nằm ngoài (O)
a) Biết AB=CD chứng minh MA=MC.
b) Nếu AB>CD, hãy so sánh khoảng cách từ điểm M đến trung điểm của các dây AB, CD
Cho đường tròn tâm O bán kính R, hai dây cung AB và CD, các tia BA và DC cắt nhau tại M nằm ngoài (O)
a) Biết AB=CD chứng minh MA=MC
b) Nếu AB>CD, hãy so sánh khoảng cách từ điểm M đến trung điểm của các dây AB, CD
Cho đường tròn(O), dây AB và dây CD, AB < CD. Giao điểm K của các đường thẳng AB, CD nằm ngoài đường tròn. Đường tròn (O;OK) cắt KA và KC tại M và N.
Chứng minh KM < KN.
Kẻ OI ⊥AB, OE ⊥ CD.
Xét đường tròn (O;OA) có: AB và CD là dây cung, AB < CD. Suy ra OI > OE.
Xét đường tròn (O;OK) có KN và KM là dây cung và OI > OE. Suy ra KM < KN.
Đúng 0
Bình luận (0)
Cho đường tròn (O), dây AB và dây CD, AB < CD. Giao điểm K của các đường thnawgr AB, CD nằm ngoài đường tròn. Đường tròn (O; OK) cắt KA và KC tại M và N
Chứng minh rằng KM < KN
