1:

a: \(\left(2x-5\right)^2-4x\left(x+3\right)\)

\(=4x^2-20x+25-4x^2-12x\)

=-32x+25

b: \(\left(x-2\right)^3-6\left(x+4\right)\left(x-4\right)-\left(x-2\right)\left(x^2+2x+4\right)\)

\(=x^3-6x^2+12x-8-\left(x^3-8\right)-6\left(x^2-16\right)\)

\(=-6x^2+12x-6x^2+96=-12x^2+12x+96\)

c: \(\left(x-1\right)^2-2\left(x-1\right)\left(x+2\right)+\left(x+2\right)^2+5\left(2x-3\right)\)

\(=\left(x-1-x-2\right)^2+5\left(2x-3\right)\)

\(=\left(-3\right)^2+5\left(2x-3\right)\)

\(=9+10x-15=10x-6\)

2: 

a: \(\left(2-3x\right)^2-5x\left(x-4\right)+4\left(x-1\right)\)

\(=9x^2-12x+4-5x^2+20x+4x-4\)

\(=4x^2+12x\)

b: \(\left(3-x\right)\left(x^2+3x+9\right)+\left(x-3\right)^3\)

\(=27-x^3+x^3-9x^2+27x-27\)

\(=-9x^2+27x\)

c: \(\left(x-4\right)^2\left(x+4\right)-\left(x-4\right)\left(x+4\right)^2+3\left(x^2-16\right)\)

\(=\left(x-4\right)\left(x+4\right)\left(x-4-x-4\right)+3\left(x^2-16\right)\)

\(=\left(x^2-16\right)\left(-8\right)+3\left(x^2-16\right)\)

\(=-5\left(x^2-16\right)=-5x^2+80\)

a: Ta có: \(\left(x+2\right)\left(x^2-2x+4\right)-x\left(x^2+2\right)=15\)

\(\Leftrightarrow x^3+8-x^3-2x=15\)

\(\Leftrightarrow2x=-7\)

hay \(x=-\dfrac{7}{2}\)

b: Ta có: \(\left(x-2\right)^3-\left(x-4\right)\left(x^2+4x+16\right)+6\left(x+1\right)^2=49\)

\(\Leftrightarrow x^3-6x^2+12x-8-x^3+64+6\left(x+1\right)^2=49\)

\(\Leftrightarrow-6x^2+12x+56+6x^2+12x+6=49\)

\(\Leftrightarrow24x=-13\)

hay \(x=-\dfrac{13}{24}\)

Câu d đề có đúng ko bn

mk thấy hơi sai Nguyen Thi tuong Vi

1a) -3x²(2x³ - 2x + 1/3) = -6x⁵ + 6x³ - x²

b) (x⁴ + 2x³ - 2/3).(-3x⁴) = -3x⁸ - 6x⁷ + 2x⁴

c) (x + 3)(x - 4) = x² - 4x + 3x - 12 = x² - x - 12

d)(x - 4)(x² + 4x + 16) = (x - 4)(x² + 4x + 4²) = x³ - 64

e) 4(x - 1/2)(x + 1/2)(4x² + 1) =4(x² - 1/4)(4x²  + 1) = 4(4x⁴ + x² - x² - 1/4) = 4(4x⁴ - 1/4) = 16x⁴ - 1

B2. a) (2 - x)(x² + 2x + 4) + x(x - 3)(x + 4) - x² + 24 = 0

=> 8 - x³ + x(x² + 4x - 3x - 12) - x² + 24 = 0

=> 8 - x³ + x³ + x² - 12x - x² + 24 = 0

=> -12x + 32 = 0

=> -12x = -32

=> x = -32 : (-12) = 8/3

b) (x/2 + 3)(5 - 6x) + (12x - 2)(x/4 + 3) = 0

=> 5x/2 - 3x² + 15 - 18x + 3x² + 36x - x/2 - 6 = 0

=> 20x + 9 = 0

=> 20x = -9

=> x = -9/20

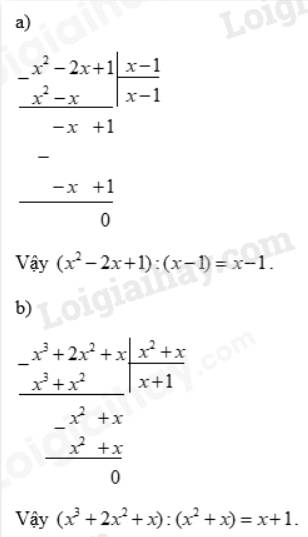
Vậy \(( - 32{x^5} + 1):( - 2x + 1) = 16{x^4} + 8{x^3} + 4{x^2} + 2x + 1\).

Bài 1.

\( a)\dfrac{{4x - 8}}{{2{x^2} + 1}} = 0 (x \in \mathbb{R})\\ \Leftrightarrow 4x - 8 = 0\\ \Leftrightarrow 4x = 8\\ \Leftrightarrow x = 2\left( {tm} \right)\\ b)\dfrac{{{x^2} - x - 6}}{{x - 3}} = 0\left( {x \ne 3} \right)\\ \Leftrightarrow \dfrac{{{x^2} + 2x - 3x - 6}}{{x - 3}} = 0\\ \Leftrightarrow \dfrac{{x\left( {x + 2} \right) - 3\left( {x + 2} \right)}}{{x - 3}} = 0\\ \Leftrightarrow \dfrac{{\left( {x + 2} \right)\left( {x - 3} \right)}}{{x - 3}} = 0\\ \Leftrightarrow x - 2 = 0\\ \Leftrightarrow x = 2\left( {tm} \right) \)

Bài 2.

\(c)\dfrac{{x + 5}}{{3x - 6}} - \dfrac{1}{2} = \dfrac{{2x - 3}}{{2x - 4}}\)

ĐK: \(x\ne2\)

\( Pt \Leftrightarrow \dfrac{{x + 5}}{{3x - 6}} - \dfrac{{2x - 3}}{{2x - 4}} = \dfrac{1}{2}\\ \Leftrightarrow \dfrac{{x + 5}}{{3\left( {x - 2} \right)}} - \dfrac{{2x - 3}}{{2\left( {x - 2} \right)}} = \dfrac{1}{2}\\ \Leftrightarrow \dfrac{{2\left( {x + 5} \right) - 3\left( {2x - 3} \right)}}{{6\left( {x - 2} \right)}} = \dfrac{1}{2}\\ \Leftrightarrow \dfrac{{ - 4x + 19}}{{6\left( {x - 2} \right)}} = \dfrac{1}{2}\\ \Leftrightarrow 2\left( { - 4x + 19} \right) = 6\left( {x - 2} \right)\\ \Leftrightarrow - 8x + 38 = 6x - 12\\ \Leftrightarrow - 14x = - 50\\ \Leftrightarrow x = \dfrac{{27}}{5}\left( {tm} \right)\\ d)\dfrac{{12}}{{1 - 9{x^2}}} = \dfrac{{1 - 3x}}{{1 + 3x}} - \dfrac{{1 + 3x}}{{1 - 3x}} \)

ĐK: \(x \ne -\dfrac{1}{3};x \ne \dfrac{1}{3}\)

\( Pt \Leftrightarrow \dfrac{{12}}{{1 - 9{x^2}}} - \dfrac{{1 - 3x}}{{1 + 3x}} - \dfrac{{1 + 3x}}{{1 - 3x}} = 0\\ \Leftrightarrow \dfrac{{12}}{{\left( {1 - 3x} \right)\left( {1 + 3x} \right)}} - \dfrac{{1 - 3x}}{{1 + 3x}} - \dfrac{{1 + 3x}}{{1 - 3x}} = 0\\ \Leftrightarrow \dfrac{{12 - {{\left( {1 - 3x} \right)}^2} - {{\left( {1 + 3x} \right)}^2}}}{{\left( {1 - 3x} \right)\left( {1 + 3x} \right)}} = 0\\ \Leftrightarrow \dfrac{{12 + 12x}}{{\left( {1 - 3x} \right)\left( {1 + 3x} \right)}} = 0\\ \Leftrightarrow 12 + 12x = 0\\ \Leftrightarrow 12x = - 12\\ \Leftrightarrow x = - 1\left( {tm} \right) \)

Bài 2.

\(a)5 + \dfrac{{96}}{{{x^2} - 16}} = \dfrac{{2x - 1}}{{x + 4}} - \dfrac{{3x - 1}}{{4 - x}}\)

ĐK: \(x\ne\pm4\)

\( Pt \Leftrightarrow \dfrac{{96}}{{\left( {x - 4} \right)\left( {x + 4} \right)}} - \dfrac{{2x - 1}}{{x + 4}} - \dfrac{{3x - 1}}{{x - 4}} = - 5\\ \Leftrightarrow \dfrac{{96 - \left( {2x - 1} \right)\left( {x - 4} \right) - \left( {3x - 1} \right)\left( {x + 4} \right)}}{{\left( {x - 4} \right)\left( {x + 4} \right)}} = - 5\\ \Leftrightarrow \dfrac{{ - 5{x^2} - 2x + 96}}{{\left( {x - 4} \right)\left( {x + 4} \right)}} = - 5\\ \Leftrightarrow - 5{x^2} - 2x + 96 = - 5\left( {{x^2} - 16} \right)\\ \Leftrightarrow 96 - 2x = 80\\ \Leftrightarrow - 2x = - 16\\ \Leftrightarrow x = 8\left( {tm} \right)\\ b)\dfrac{{3x + 2}}{{3x - 2}} - \dfrac{6}{{2 + 3x}} = \dfrac{{9{x^2}}}{{9{x^2} - 4}} \)

ĐK: \(x \ne \dfrac{2}{3};x \ne -\dfrac{2}{3}\)

\( Pt \Leftrightarrow \dfrac{{3x + 2}}{{3x - 2}} - \dfrac{6}{{2 + 3x}} - \dfrac{{9{x^2}}}{{9{x^2} - 4}} = 0\\ \Leftrightarrow \dfrac{{{{\left( {2 + 3x} \right)}^2} - 6\left( {3x - 2} \right) - 9{x^2}}}{{\left( {3x - 2} \right)\left( {2 + 3x} \right)}} = 0\\ \Leftrightarrow \dfrac{{16 - 6x}}{{\left( {3 - 2x} \right)\left( {2 + 3x} \right)}} = 0\\ \Leftrightarrow 16 - 6x = 0\\ \Leftrightarrow - 6x = - 16\\ \Leftrightarrow x = \dfrac{8}{3}\left( {tm} \right)\\ c)\dfrac{{x + 1}}{{{x^2} + x + 1}} - \dfrac{{x - 1}}{{{x^2} - x + 1}} = \dfrac{3}{{x\left( {{x^4} + {x^2} + 1} \right)}} \)

Ta có: \(x(x^4+x^2+1)=x[(x^2+1)^2-x^2]=x(x^2+x+1)(x^2-x+1)\)

Do \(\left\{ \begin{array}{l} {x^2} + x + 1 = {\left( {x + \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} > 0\forall x\\ {x^2} - x + 1 = \left( {x - \dfrac{1}{2}} \right) + \dfrac{3}{4} > 0\forall x \end{array} \right.\) nên phương trình xác định với mọi $x \ne 0$

Quy đồng, rồi biến đổi phương trình về dạng \(2x=3 \Leftrightarrow x =\dfrac{3}{2} (tm)\)