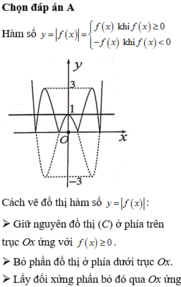
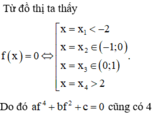Lấy một ví dụ về hàm số dạngy = ax4 + bx2 + c sao cho phương trình y’ = 0 chỉ có một nghiệm.

Những câu hỏi liên quan
Trả lời câu hỏi Toán 12 Giải tích Bài 5 trang 38: Lấy một ví dụ về hàm số dạng y = ax4 + bx2 + c sao cho phương trình y’ = 0 chỉ có một nghiệm.
Ví dụ: Hàm số y = x4 + 2x2 có y' = 4x3 + 4x
Phương trình y' = 0 chỉ có một nghiệm x = 0
Đúng 1
Bình luận (1)
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị như hình vẽ bên. Số nghiệm của phương trình
f
x
+
3
0
là A. 4 B. 3 C. 1 D. 2
Đọc tiếp
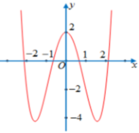
Cho hàm số y = a x 4 + b x 2 + c có đồ thị như hình vẽ bên. Số nghiệm của phương trình f x + 3 = 0 là
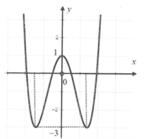
A. 4
B. 3
C. 1
D. 2
Đáp án D
![]()
Số nghiệm phương trình (*) là số giao điểm của đồ thị y = f(x) và đường thẳng y = -3
Dựa vào đồ thị thấy có 2 giao điểm suy ra phương trình (*) có 2 nghiệm
Số nghiệm phương trình (*) là số giao điểm của đồ thị y = f(x) và đường thẳng y = -3
Dựa vào đồ thị thấy có 2 giao điểm suy ra phương trình (*) có 2 nghiệm
Đúng 0
Bình luận (0)
Cho hàm số y = f x = a x 4 + b x 2 + c có đồ thị như hình vẽ. Số nghiệm của phương trình f(x)+3 = 0
là
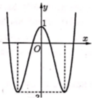
Chọn đáp án D.
Ta có f(x)+3 = 0 → f(x) = -3 dựa vào đồ thị hàm số suy ra phương trình này có 2 nghiệm phân biệt.
Đúng 0
Bình luận (0)
Cho hàm số
y
f
(
x
)
a
x
4
+
b
x
2
+
c
(
a
≠
0
)
có đồ thị như hình bên. Tất cả các giá trị của m để phương trình
f
x
+
m
+
1
0
có 7 nghiệm phân biệt là: A. m...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 4 + b x 2 + c ( a ≠ 0 ) có đồ thị như hình bên. Tất cả các giá trị của m để phương trình f x + m + 1 = 0 có 7 nghiệm phân biệt là:
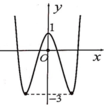
A. m = -2
B. m = -1
C. m = 2
D. m = 0
Cho hàm số
f
x
a
x
4
+
b
x
2
+
c
có đồ thị như hình vẽ bên. Hỏi phương trình
a
.
f
4
x
+
b
.
f
2
x
+
c
0
có bao nhiêu nghiệm thực phân biệt? A. 4. B. 15. ...
Đọc tiếp
Cho hàm số f x = a x 4 + b x 2 + c có đồ thị như hình vẽ bên. Hỏi phương trình a . f 4 x + b . f 2 x + c = 0 có bao nhiêu nghiệm thực phân biệt?
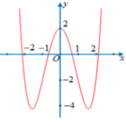
A. 4.
B. 15.
C. 14.
D. 16.
Cho hàm số
f
x
a
x
4
+
b
x
2
+
c
có đồ thị như hình vẽ bên. Hỏi phương trình
a
.
f
4
x
+
b
.
f
2
x
+
c
0
có bao nhiêu nghiệm thực phân biệt? A. 4 B. 15...
Đọc tiếp
Cho hàm số f x = a x 4 + b x 2 + c có đồ thị như hình vẽ bên. Hỏi phương trình a . f 4 x + b . f 2 x + c = 0 có bao nhiêu nghiệm thực phân biệt?
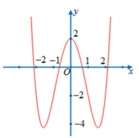
A. 4
B. 15
C. 14
D. 16
Cho hàm số
y
f
(
x
)
a
x
4
+
b
x
2
+
c
(
a
≠
0
)
có đồ thị như hình bên. Tất cả các giá trị của m để phương trình
f
(
x
)
+
m
+
1
0...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 4 + b x 2 + c ( a ≠ 0 ) có đồ thị như hình bên. Tất cả các giá trị của m để phương trình f ( x ) + m + 1 = 0 có 7 nghiệm phân biệt là:
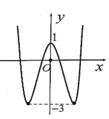
A. m=-2.
B. m=-1.
C. m=2.
D. m=0.
Hàm số
f
(
x
)
a
x
4
+
b
x
2
+
c
(
a
,
b
,
c
∈
ℝ
)
có đồ thị như hình vẽ Số nghiệm thực của phương trình 2f(x) -3 0 bằng A. 0 B. 3 C. 2 D. 4
Đọc tiếp
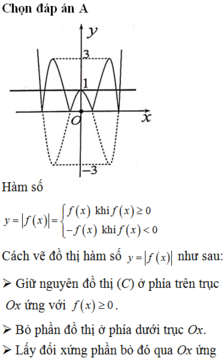
Hàm số f ( x ) = a x 4 + b x 2 + c ( a , b , c ∈ ℝ ) có đồ thị như hình vẽ
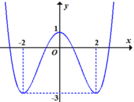
Số nghiệm thực của phương trình 2f(x) -3 =0 bằng
A. 0
B. 3
C. 2
D. 4
Cho hàm số
f
(
x
)
a
x
4
+
b
x
2
-
1
(
a
,
b
∈
ℝ
)
. Đồ thị của hàm số yf(x) như hình vẽ bên. Số nghiệm thực của phương trình 2018.f(x) + 2019 0 là: A. 4 B. 0 C. 3 D. 2
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 2 - 1 ( a , b ∈ ℝ ) . Đồ thị của hàm số y=f(x) như hình vẽ bên. Số nghiệm thực của phương trình 2018.f(x) + 2019 = 0 là:
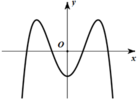
A. 4
B. 0
C. 3
D. 2